题目内容
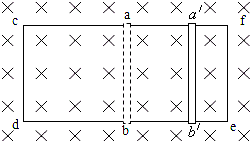
 如图所示,有一长2米,宽0.5米的长方形金属框cdef,在它上面放置一根直导线ab,导线在框架上无摩擦地滑动,框架的导线都是用0.1欧/米的导体材料做成,整个框架置于磁感强度B为1.04特的匀强磁场中.让导线ab从框架中央位置开始以V=0.25米/秒的速度向右匀速运动,到达a′b′位置(bb′=0.75米)时,问:(1)此时导线ab中产生的感应电动势大小?
如图所示,有一长2米,宽0.5米的长方形金属框cdef,在它上面放置一根直导线ab,导线在框架上无摩擦地滑动,框架的导线都是用0.1欧/米的导体材料做成,整个框架置于磁感强度B为1.04特的匀强磁场中.让导线ab从框架中央位置开始以V=0.25米/秒的速度向右匀速运动,到达a′b′位置(bb′=0.75米)时,问:(1)此时导线ab中产生的感应电动势大小?(2)此时导线ab中感应电流多大?
(3)当导线ab从框架中央位置到达a′b′位置的过程中,导线ab所受的外力F发生怎样的变化?
分析:(1)导线ab向右运动,切割磁感线产生感应电动势,相当于电源,画出等效电路图.由E=BLv求出感应电动势;
(2)由题中条件求出电路中的电阻,根据闭合电路欧姆定律求解感应电流;
(3)由F安=BIL,I=
,E=BLv推导出安培力表达式,导线匀速运动,外力F与安培力平衡,即可得到外力F的表达式,再进行分析.
(2)由题中条件求出电路中的电阻,根据闭合电路欧姆定律求解感应电流;
(3)由F安=BIL,I=
| E |
| R总 |
解答: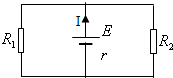 解:画出等效电路图:
解:画出等效电路图:
(1)导线ab中产生的感应电动势为 E=BLv=0.13(V)
(2)R1=(0.5+1.75+1.75)×0.1=0.4(Ω)
R2=(0.5+0.25+0.25)×0.1=0.1(Ω)
R1与R2并联电阻为R12=
=0.08(Ω),r=0.5×0.1=0.05(Ω)
则由闭合电路欧姆定律得 I=
=1(A)
(3)外力 F外=F安=BIL=B
L=
外电路总电阻为 R总=
根据数学知识得知,当t=0时 R总最大
所以当金属棒移动时R总在减小,则F外在增大
答:
(1)此时导线ab中产生的感应电动势大小为0.13V.
(2)此时导线ab中感应电流为1A.
(3)当导线ab从框架中央位置到达a′b′位置的过程中,导线ab所受的外力F在增大.
 解:画出等效电路图:
解:画出等效电路图:(1)导线ab中产生的感应电动势为 E=BLv=0.13(V)
(2)R1=(0.5+1.75+1.75)×0.1=0.4(Ω)
R2=(0.5+0.25+0.25)×0.1=0.1(Ω)
R1与R2并联电阻为R12=
| R1R2 |
| R1+R2 |
则由闭合电路欧姆定律得 I=
| E |
| R12+r |
(3)外力 F外=F安=BIL=B
| E |
| R总 |
| B2L2v |
| R总 |
外电路总电阻为 R总=
| (R10+kvt)(R20-kvt) |
| R10+R20 |
根据数学知识得知,当t=0时 R总最大
所以当金属棒移动时R总在减小,则F外在增大
答:
(1)此时导线ab中产生的感应电动势大小为0.13V.
(2)此时导线ab中感应电流为1A.
(3)当导线ab从框架中央位置到达a′b′位置的过程中,导线ab所受的外力F在增大.
点评:本题通过画出等效电路图,就能很容易地求出外电路总电阻,要掌握安培力的推导方法,即可分析外力的变化情况.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目