题目内容
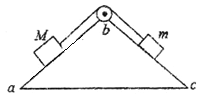
【题目】如图所示,楔形木块abc固定在水平面上,粗糙斜面ab和光滑斜面bc与水平面的夹角相同,顶角b处安装一定滑轮。质量分别为M、m(M>m)的滑块,通过不可伸长的轻绳跨过定滑轮连接,轻绳与斜面平行。两滑块由静止释放后,沿斜面做匀加速运动.若不计滑轮的质量和摩擦,在两滑块沿斜面运动的过程中
A. 两滑块组成系统的机械能损失小于M克服摩擦力做的功
B. M所受轻绳拉力与重力的总功等于M动能的增加
C. 绳对m做的功大于m动能的增加
D. 轻绳对M做的功大于轻绳对m做的功
【答案】C
【解析】
根据滑块质量关系确定滑块的滑动方向,然后根据滑块的受力情况应用动能定理与能量守恒定律分析答题。
由题意可知,M>m,释放后,滑块M向下滑动,m沿斜面向上滑动;
A项:除重力弹力以外的力做功,将导致机械能变化,摩擦力做负功,造成机械能损失,则有:两滑块组成系统的机械能损失等于M克服摩擦力做的功,故A错误;
B项:由动能定理可知,M所受轻绳的拉力、重力与摩擦力的做总功等于M动能的增加量,M所受轻绳拉力与重力的总功大于M动能的增加,故B错误;
C项:m向上滑动,由动能定理可知,轻绳对m做的功大于m动能增加,故C正确;
D项:轻绳对M与对m的拉力大小相等,M与m的位移大小相等,轻绳对M与对m的拉力做功相等,故D错误。
故选:C。

 阳光课堂课时优化作业系列答案
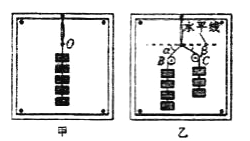
阳光课堂课时优化作业系列答案【题目】某实验小组利用下图甲所示器材测量滑块与木板之间的动摩擦因素。
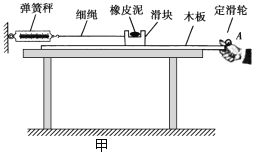
实验步骤:
①用弹簧秤测量橡皮泥和滑块的总重力,记作G;
②将装有橡皮泥的滑块放在水平木板上,通过水平细绳和固定弹簧秤相连,如图所示。在A端向右水平拉动木板,待弹簧秤示数稳定后,将读数记作F;
③改变滑块上橡皮泥的质量,重复步骤①②;
实验数据如下表所示:
次数 力 | 1 | 2 | 3 | 4 | 5 | 6 |
G/N | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 |
F/N | 0.59 | 0.83 | 0.99 | 1.22 | 1.37 | 1.61 |
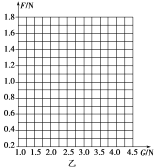
(1)根据表中数据在图乙坐标纸上作出F-G图线___________。
(2)由图线求得滑块和木板间的动摩擦因数μ=________(保留两位有效数字)。
(3)在A端向右水平拉动木板速度的大小对动摩擦因数的测量____________(选填“会”或“不会”)产生影响。