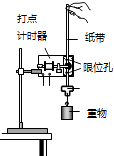
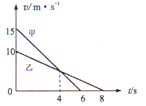
��Ŀ����
����Ŀ��һ��С��ͣ����ˮƽ�����ϣ��������Ⱦ�Ϊl��ϸ�߷ֱ�����С��A�����B������ϸ������ֱ��ˮƽ����ֱ��300�ǣ���ͼ��ʾ����֪���B��������С��A���������Ҵ�ʱ���B�պ��ܾ�ֹ����֪�������ٶ�Ϊg�������Ħ�������ڻ���Ħ������
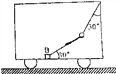
��1�������B��С���װ��Ķ�Ħ�������̣�
��2�������B�̶���С���װ�ԭ����λ�ã�����С���ص����������ȼ���ֱ���˶�����A��B��ϸ������Ϊ�㣬��С�����ٶ�Ӧ����ʲô������
���𰸡���1��![]() ��2��
��2��![]()
����������1����С��A������Ϊm��������B������Ϊ2m����BΪ�о��������������������ͼ��ʾ��

ˮƽ������ݹ�������ƽ�������ɵã�FBcos30��=��N1��
��ֱ������ݹ�������ƽ�������ɵã�N1=2mg-FBsin30�㣬
���ݻ���Ħ�����ļ��㹫ʽ�ɵã�f=��N1��
������ã�FBcos30��=�̣�2mg-FBsin30�㣩��
��С��������С��A����������ΪFA������Ϊ�о����ɵã�
FAcos60��=�̣�3mg-FAsin60�㣩��
����С��AΪ�о�������ֱ��������ƽ��ɵã�
FAsin60��=mg+FBsin30���
�����٢ڢۿɵã���=![]() ��
��
��2����AΪ�о�����AB������Ϊ��ʱ��С���ٶ�Ϊa1�����ܹ�ţ�ٵڶ����ɿɵã�
mgtan30��=ma1����ã�a1=gtan30��=![]() g��
g��
���ż��ٶȵ�����ABϸ����ˮƽ����ļн�������AB��ˮƽ��������60��ʱ��ABϸ���ٴ���ֱ����ʱ���ٶ�Ϊa2������ʱ��С��A��ϸ������ֱ����ļн�Ϊ60�㣬��A�����ţ�ٵڶ����ɿɵã�a2=gtan60��=![]() g���������������ļ��ٶ�Ϊ
g���������������ļ��ٶ�Ϊ![]() g��a��
g��a��![]() g��
g��