题目内容
(9分)一质量为M=10kg的木板B静止于光滑水平面上,其上表面粗糙,物块A质量为m=6kg,停在B的左端。质量为m0=1kg的小球用长为l=0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为h=0.2m,物块与小球可视为质点,g取10m/s2,不计空气阻力。

①求碰撞结束时A的速度;
②若木板B足够长,A最终没有滑离B,求A在B上滑动的过程中系统损失的机械能。
【答案】
(1)1m/s;(2)1.875J
【解析】
试题分析:①设小球运动到最低点的速度为v0,由机械能守恒定律
 ,代入数据解得:v0=4m/s。(1分)
,代入数据解得:v0=4m/s。(1分)
设碰撞结束后小球的速度大小为v1,A的速度大小为v2,
碰撞结束后小球反弹上升,由机械能守恒有:
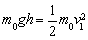 ,代入数据解得:v1=2m/s。(1分)
,代入数据解得:v1=2m/s。(1分)
对碰撞过程,由动量守恒有:m0v0=-m0v1+mv2
将v0、v1结果代入得v2=1m/s,方向水平向右(3分)
②经分析知,最后A没有滑离B,A、B共同运动,设共同运动速度为v3,
对A、B系统,由动量守恒得mv2=(m+M)v3,解得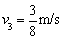
此过程中损失的机械能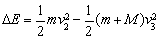 (2分)
(2分)
把第①问的v2代入以上两式解得: (或者1.875J)。(2分)
(或者1.875J)。(2分)
考点:动量守恒定律,能量守恒

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 除此之外,不记其他损耗。求电动机由于传送工件多消耗的电能。(取g=10 m/s2)
除此之外,不记其他损耗。求电动机由于传送工件多消耗的电能。(取g=10 m/s2)
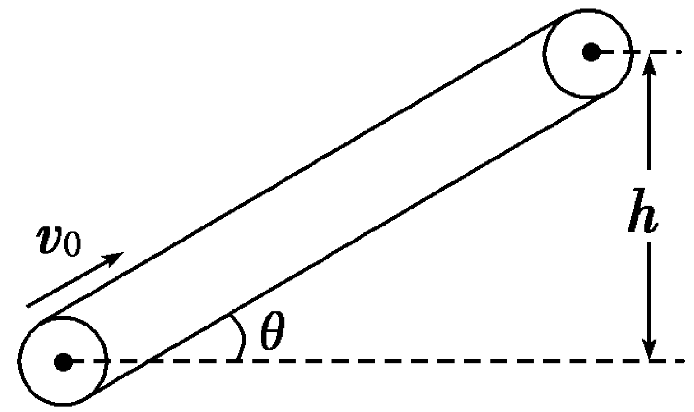
 动下,始终保持v0=2m/s的速率运行。现把一质量为m=10kg的工件(可视为质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求:
动下,始终保持v0=2m/s的速率运行。现把一质量为m=10kg的工件(可视为质点)轻轻放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,取g=10m/s2。求: