题目内容
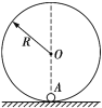
【题目】如图所示，内壁光滑半径大小为R的圆轨道竖直固定在桌面上，一个质量为m的小球静止在轨道底部A点。现用小锤沿水平方向快速击打小球，击打后迅速移开，使小球沿轨道在竖直面内运动。当小球回到A点时，再次用小锤沿运动方向击打小球。必须经过两次击打，小球才能运动到圆轨道的最高点。已知小球在运动过程中始终未脱离轨道，在第一次击打过程中小锤对小球做功W，第二次击打过程中小锤对小球做功4W。设两次击打过程中小锤对小球做的功全部用来增加小球的动能，则W的值可能是 （ ）
A.
mgRB.
mgRC.
mgRD.
mgR
【答案】AB
【解析】
小球在竖直面内运动只有重力做功，故机械能守恒，小球要到达圆轨道最高点，那么，对小球在最高点应用牛顿第二定律可得
所以，小球的机械能
小球在运动过程中始终未脱离轨道，且必须经过两次击打，小球才能运动到圆轨道的最高点，故第一次击打后，小球运动的高度不大于R，所以有
解得
故AB正确，CD错误。
故选AB。
练习册系列答案
阅读快车系列答案
相关题目
