题目内容
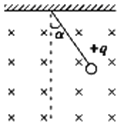
【题目】如图所示，水平面内的等边三角形ABC的边长为L，顶点C恰好位于光滑绝缘直轨道DC的最低点，光滑直导轨上端点D到A、B两点的距离均为L，D在AB边上的竖直投影点为O．一对电荷量均为-Q的点电荷分别固定于A、B两点．在D处将质量为m、电荷量为+q的小球套在轨道上（忽略它对原电场的影响），将小球由静止开始释放，已知静电力常量为k、重力加速度为g，且
，忽略空气阻力，则
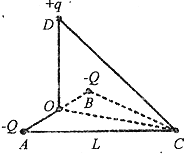
A. D点的电场强度与C点的大小相等
B. 小球沿直轨道DC向下做匀加速直线运动
C. 小球刚到达C点时，加速度为零
D. 小球沿直轨道DC下滑过程中，其电势能先增大后减小
【答案】AC
【解析】由几何关系可知，DC两点到两个电荷的距离均相等，由场强叠加可知，D点的电场强度与C点的大小相等，选项A正确；小球沿直轨道DC向下滑动的过程中距离两点荷的距离先减小后增加，则所受的电场力不是定值，则合力不是定值，则小球不是做匀加速直线运动，选项B错误；负电荷产生的电场指向负电荷，可知两个负电荷在D处的电场强度分别指向A与B，由于两个点电荷的电量是相等的，所以两个点电荷在D点的电场强度的大小相等，则它们的合场强的方向沿DA、DB的角平分线；由库仑定律，A、B在D点的场强的大小：EA＝EB＝
；它们的合场强：ED=EAcos30°+EBcos30°=
；由几何关系宽度：DO=OC=
L，则：∠OCD=45°.
对小球进行受力分析，其受力的剖面图如图：由于C到A、B的距离与D到A、B的距离都等于L，结合A的分析可知，C点的电场强度的大小与D点的电场强度的大小相等，方向指向O点，即：EC＝ED＝，沿斜面方向：mgcos45°-Fcos45°=ma；垂直于方向：mgsin45°+Fsin45°=N；其中F是库仑力，F=qEC=mg，联立以上三式得：a=0．故C正确；由几何关系可知，在CD的连线上，CD连线的中点处于到A、B的距离最小，电势最低，小球带正电，所以小球在CD的连线中点处的电势能最小．则小球沿直轨道CD下滑过程中，其电势能先减小后增大．故D错误；故选AC．
