题目内容
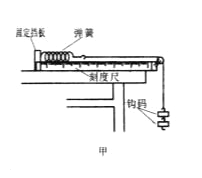
【题目】(多选)如图所示,小球A可视为质点,装置静止时轻质细线AB水平,轻质细线AC与竖直方向的夹角θ=37°.已知小球的质量为m,细线AC长l,B点距C点的水平和竖直距离相等.装置BO′O能以任意角速度绕竖直轴O′O转动,且小球始终在BO′O平面内,那么在ω从零缓慢增大的过程中( )(g取10m/s2,sin 37°=0.6,cos 37°=0.8)

A. 两细线张力均增大
B. 细线AB中张力一直变小,直到为零
C. 细线AC中张力先不变,后增大
D. 当AB中张力为零时,角速度可能为![]()
【答案】CD
【解析】当静止时,受力分析如右图,由平衡条件

TAB=mgtan37°=0.75mg,TAC=![]() =1.25mg,
=1.25mg,
若AB中的拉力为0,当ω最小时绳AC与竖直方向夹角θ1=37°,受力分析如右图,mgtanθ1=m(lsinθ1)ωmin2,得ωmin=![]() .
.

当ω最大时绳AC与竖直方向夹角θ2=53°,mgtanθ2=mωmax2lsinθ2,得ωmax=![]() .所以ω取值范围为
.所以ω取值范围为![]() ≤ω≤
≤ω≤![]() .绳子AB的拉力都是0.由以上的分析可知,开始时AB是拉力不为0,当转速在
.绳子AB的拉力都是0.由以上的分析可知,开始时AB是拉力不为0,当转速在![]() ≤ω≤
≤ω≤![]() 时,AB的拉力为0,角速度再增大时,AB的拉力又会增大,故AB错误;当绳子AC与竖直方向之间的夹角不变时,AC绳子的拉力在竖直方向的分力始终等于重力,所以绳子的拉力绳子等于1.25mg;当转速大于
时,AB的拉力为0,角速度再增大时,AB的拉力又会增大,故AB错误;当绳子AC与竖直方向之间的夹角不变时,AC绳子的拉力在竖直方向的分力始终等于重力,所以绳子的拉力绳子等于1.25mg;当转速大于![]() 后,绳子与竖直方向之间的夹角增大,拉力开始增大;当转速大于
后,绳子与竖直方向之间的夹角增大,拉力开始增大;当转速大于![]() 后,绳子与竖直方向之间的夹角不变,AC上竖直方向的拉力不变当水平方向的拉力增大,AC的拉力继续增大;故C正确;由开始时的分析可知,当ω取值范围为
后,绳子与竖直方向之间的夹角不变,AC上竖直方向的拉力不变当水平方向的拉力增大,AC的拉力继续增大;故C正确;由开始时的分析可知,当ω取值范围为![]() ≤ω≤
≤ω≤![]() .绳子AB的拉力都是0.故D正确.故选CD.
.绳子AB的拉力都是0.故D正确.故选CD.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目