题目内容
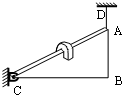 如图所示,质量分布均匀的直角三角板ABC重为20N,可绕过C点、垂直于板面的水平转动轴自由转动,A点用竖直线AD拉住,当BC处于水平平衡位置时AD线上的拉力大小为F.后将一块凹槽口朝下、重为4N的物块卡在斜边AC上,物块沿斜边AC匀加速下滑,当物块经过AC的中点时细线的拉力大小变为F+△F,则下述结论中正确的是
如图所示,质量分布均匀的直角三角板ABC重为20N,可绕过C点、垂直于板面的水平转动轴自由转动,A点用竖直线AD拉住,当BC处于水平平衡位置时AD线上的拉力大小为F.后将一块凹槽口朝下、重为4N的物块卡在斜边AC上,物块沿斜边AC匀加速下滑,当物块经过AC的中点时细线的拉力大小变为F+△F,则下述结论中正确的是
- A.F=10N
- B.F<10N
- C.△F>2N
- D.△F=2N
D
分析:质量分布均匀的直角三角板的重心在靠近AB的位置,根据杠杆平衡条件可得F的大小;△F的大小计算,设角ACB为θ,木块对斜面的压力为FN=mg?cosθ=4cosθ,对于三角板,再次运用杠杆平衡条件得到绳子拉力大小.
解答:A、B、质量分布均匀的三角形的重心在靠近AB的位置,以C点为支点,根据杠杆平衡条件可得
Mg?l1=F?lBC ①
由于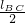 <l1<lBC
<l1<lBC
解得
F>10N
故A、B均错误;
C、D、△F的大小计算,设角ACB为θ,将三角板的重力忽略,木块对斜面的压力为
FN=mg?cosθ=4cosθ
对于三角板,由杠杆平衡条件得
4cosa?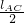 +Mg?l1=(F+△F)?lBC ②
+Mg?l1=(F+△F)?lBC ②
由①②两式得到,△F=2N
故C错误,D正确;
故选D.
点评:本题关键根据力矩平衡条件列式分析计算,同时要知道三角形的重心为三个中线的交点.
分析:质量分布均匀的直角三角板的重心在靠近AB的位置,根据杠杆平衡条件可得F的大小;△F的大小计算,设角ACB为θ,木块对斜面的压力为FN=mg?cosθ=4cosθ,对于三角板,再次运用杠杆平衡条件得到绳子拉力大小.
解答:A、B、质量分布均匀的三角形的重心在靠近AB的位置,以C点为支点,根据杠杆平衡条件可得
Mg?l1=F?lBC ①
由于
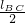 <l1<lBC
<l1<lBC解得
F>10N
故A、B均错误;
C、D、△F的大小计算,设角ACB为θ,将三角板的重力忽略,木块对斜面的压力为
FN=mg?cosθ=4cosθ
对于三角板,由杠杆平衡条件得
4cosa?
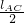 +Mg?l1=(F+△F)?lBC ②
+Mg?l1=(F+△F)?lBC ②由①②两式得到,△F=2N
故C错误,D正确;
故选D.
点评:本题关键根据力矩平衡条件列式分析计算,同时要知道三角形的重心为三个中线的交点.

练习册系列答案
相关题目