题目内容
7. 两根长直轨道与一半径为R的半圆型圆弧轨道相接于A、C两点,B点为轨道 最低点,O为圆心,轨道各处光滑且固定在竖直平面内,质量均为m的两小环P、Q用长为$\sqrt{2}$R的轻杆连接在一起,套在轨道上.将P、Q两环从距B点竖直距离为2R处由静止释放,假设整个过程中轻杆和轨道始终不接触,重力加速度为g,求:
两根长直轨道与一半径为R的半圆型圆弧轨道相接于A、C两点,B点为轨道 最低点,O为圆心,轨道各处光滑且固定在竖直平面内,质量均为m的两小环P、Q用长为$\sqrt{2}$R的轻杆连接在一起,套在轨道上.将P、Q两环从距B点竖直距离为2R处由静止释放,假设整个过程中轻杆和轨道始终不接触,重力加速度为g,求:(1)P环恰好到A位置时,P环的速度;
(2)P环恰好到B位置时,P环的速度;
(3)P环运动过程中的最大速度.
分析 (1)轻杆下滑过程,系统的机械能守恒,确定出两环下降的高度,即可由求得P环运动到A点时的速度;
(2)P环恰好到B位置时,两环沿杆方向的速度大小相等,得到两环速度的关系,结合系统的机械能守恒求解;
(3)当系统质心下降到最低处即轻杆水平时,系统达到的速度最大,再由机械能守恒求解.
解答 解:(1)P环恰好到A位置时,P、Q两环的速度相同,由机械能守恒定律可得:2mgR=$\frac{1}{2}•$2mv2
得:v=$\sqrt{2gR}$
(2)P环落到B位置时,P、Q丙环沿杆方向的分速度相同,根据几何关系有:
vPcos45°=vQcos45°
根据系统的机械能守恒定律得:
mg•2R+mg($\sqrt{2}$+1)R=$\frac{1}{2}m{v}_{P}^{2}$+$\frac{1}{2}m{v}_{Q}^{2}$
解得 vP=$\sqrt{(\sqrt{2}+3)gR}$
(3)P、Q两环都在半圆上运动时,沿杆方向的分速度相同,根据几何关系有:
vPcos45°=vQcos45°
可得两球的速度始终相同,vP=vQ
当轻杆恰好水平时,系统的重力势能最小,两环的速度最大.
根据系统的机械能守恒得:mgR(2+2$\sqrt{2}$)=$\frac{1}{2}•2m{v}_{P}^{2}$
解得 vP=$\sqrt{(2+2\sqrt{2})gR}$
答:(1)P环恰好到位置时,P环的速度是$\sqrt{2gR}$;
(2)P环恰好到B位置时,P环的速度是$\sqrt{(\sqrt{2}+3)gR}$;
(3)P环运动过程中的最大速度是$\sqrt{(2+2\sqrt{2})gR}$.
点评 本题关键是根据几何关系得到两环的速度关系,然后根据系统的机械能守恒定律列方程求解即可.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{v}{2}$ | B. | 2v | C. | $\frac{v}{\sqrt{2}}$ | D. | $\sqrt{2}$v |
 用密封性能良好的活塞把一定质量的理想气体封闭在导热性能良好的汽缸中,汽缸的内壁光滑.现将汽缸缓慢地由水平放置(如图甲所示)变成竖直放置(如图乙所示).在此过程中如果环境保持恒温,下列说法正确的是( )
用密封性能良好的活塞把一定质量的理想气体封闭在导热性能良好的汽缸中,汽缸的内壁光滑.现将汽缸缓慢地由水平放置(如图甲所示)变成竖直放置(如图乙所示).在此过程中如果环境保持恒温,下列说法正确的是( )| A. | 此过程吸收热量 | |
| B. | 气体分子的平均动能变大 | |
| C. | 气缸内壁单位面积上受到气体分子撞击的平均作用力不变 | |
| D. | 气缸内气体的分子数密度(单位体积内的分子数)变大 |
 如图所示为质谱仪的原理图,Ⅰ为粒子加速器,加速电压为U1:Ⅱ为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;Ⅲ为偏转分离器,磁感应强度为B2.今有一质量为m、电量为q的正离子经加速后,恰能通过速度选择器,进入分离器后在Ⅲ中做匀速圆周运动,不计粒子的重力及粒子间的相互作用.求:
如图所示为质谱仪的原理图,Ⅰ为粒子加速器,加速电压为U1:Ⅱ为速度选择器,磁场与电场正交,磁感应强度为B1,板间距离为d;Ⅲ为偏转分离器,磁感应强度为B2.今有一质量为m、电量为q的正离子经加速后,恰能通过速度选择器,进入分离器后在Ⅲ中做匀速圆周运动,不计粒子的重力及粒子间的相互作用.求: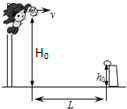 如图所示,在投球游戏中,小明坐在可沿竖直方向升降的椅子上,停在不同高度处将小球水平抛出落入固定的球框中.已知球框距地面的高度为h0,小球的质量为m,抛出点与球框的水平距离始终为L,忽略空气阻力.
如图所示,在投球游戏中,小明坐在可沿竖直方向升降的椅子上,停在不同高度处将小球水平抛出落入固定的球框中.已知球框距地面的高度为h0,小球的质量为m,抛出点与球框的水平距离始终为L,忽略空气阻力. 在一次“验证机械能守恒定律实验”中,质量M=1kg的重物自由下落,在纸带上打出一系列的点,O点为得物刚释放时打下的起始点,如图所示(相邻计数点之间的时间间隔为0.02s),单位cm,那么:
在一次“验证机械能守恒定律实验”中,质量M=1kg的重物自由下落,在纸带上打出一系列的点,O点为得物刚释放时打下的起始点,如图所示(相邻计数点之间的时间间隔为0.02s),单位cm,那么: 如图所示为某探究活动小组设计的一种节能系统:斜面轨道倾角为37°,斜面底端装有一组弹簧,弹簧不受力时其上部的自由端恰好在图中P点位置,已知P点以下的轨道光滑,P点以上的轨道与木箱之间的动摩擦因数μ=0.5.且P点以上的高度长度s=4.5m,木箱(可看成质点)的质量M=5kg,木箱在轨道顶端Q点时,自动装货装置将质量为m的货物装入木箱,木箱载着货物沿轨道无初速滑下,当木箱下滑L=5m距离时,轻弹簧被压缩至最短,此时自动装卸货装置将货物卸下,然后木箱恰好被弹回到轨道顶端Q点,再重复上述过程.g取10m/s2,不计碰撞能量损失及空气阻力.求:
如图所示为某探究活动小组设计的一种节能系统:斜面轨道倾角为37°,斜面底端装有一组弹簧,弹簧不受力时其上部的自由端恰好在图中P点位置,已知P点以下的轨道光滑,P点以上的轨道与木箱之间的动摩擦因数μ=0.5.且P点以上的高度长度s=4.5m,木箱(可看成质点)的质量M=5kg,木箱在轨道顶端Q点时,自动装货装置将质量为m的货物装入木箱,木箱载着货物沿轨道无初速滑下,当木箱下滑L=5m距离时,轻弹簧被压缩至最短,此时自动装卸货装置将货物卸下,然后木箱恰好被弹回到轨道顶端Q点,再重复上述过程.g取10m/s2,不计碰撞能量损失及空气阻力.求: 为了研究过山车的原理,某兴趣小组提出了下列设想:如图所示,取一个与水平方向夹角为θ=37°、长为L=2.0m的粗糙倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其AB与BC轨道以微小圆弧相接.一个小物块以初速度v0=4.0m/s从某一高处水平抛出,到A点时速度方向恰好沿AB方向,并沿倾斜轨道滑下,已知物体与倾斜轨道间的动摩擦因数μ=0.50.(g=10m/s2,sin37°=0.60,cos37°=0.80),求:
为了研究过山车的原理,某兴趣小组提出了下列设想:如图所示,取一个与水平方向夹角为θ=37°、长为L=2.0m的粗糙倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其AB与BC轨道以微小圆弧相接.一个小物块以初速度v0=4.0m/s从某一高处水平抛出,到A点时速度方向恰好沿AB方向,并沿倾斜轨道滑下,已知物体与倾斜轨道间的动摩擦因数μ=0.50.(g=10m/s2,sin37°=0.60,cos37°=0.80),求: