题目内容
如图所示,某小同学作滑板表演.该同学连同滑板质量为m=30kg(可视为质点),从倾角为37°的斜坡上的A点由静止开始下滑,在B点沿圆弧切线进入竖直光滑圆弧轨道.并从C点离开圆轨道腾空飞出,恰好在腾空后运动轨迹的最高点登上右侧平台.B、C为圆弧轨道的两端点,其连线水平.已知平台高h=0.8m,圆弧轨道半径为R=1.0m,斜坡与滑板间的动擦因数是0.25.不计空气阻力(g=10m/s2,sin37°=0.6,cos37°=0.8),试求:
(1)小同学登上平台时的速度;
(2)滑板在圆弧轨道最低点受到轨道的作用力大小;
(3)A、B两点间的距离.(结果保留三位有效数字)

(1)小同学登上平台时的速度;
(2)滑板在圆弧轨道最低点受到轨道的作用力大小;
(3)A、B两点间的距离.(结果保留三位有效数字)

分析:(1)该同学从C点离开圆轨道腾空飞出,恰好在腾空后运动轨迹的最高点登上右侧平台,此过程是斜上抛运动,其逆过程是平抛运动,根据高度h,由竖直方向上是自由落体运动,即可求出经过C点时竖直方向的分速度.经过C点时,该同学的速度与水平方向的夹角为37°,根据速度的分解,即可求出经过C点时水平分速度,即为小同学登上平台时的速度;
(2)由速度的合成可求出C点的速度.从B到圆弧轨道最低点的过程,机械能守恒,求出到达最低点时的速度大小,由牛顿第二定律即可求解圆弧轨道对滑板对支持力;
(3)A到B过程,运用动能定理求解A、B两点间的距离.
(2)由速度的合成可求出C点的速度.从B到圆弧轨道最低点的过程,机械能守恒,求出到达最低点时的速度大小,由牛顿第二定律即可求解圆弧轨道对滑板对支持力;
(3)A到B过程,运用动能定理求解A、B两点间的距离.
解答:解:(1)从C腾空飞出平台的过程可逆向看作平抛运动,在C点:y竖直方向的分速度为vy,水平方向分速度为x.则有
=2gh ①
又tan37°=
②
解得 vx=
≈5.33m/s,即为登上平台的速度.
(2)由sin37°=
得,vC=
m/s
从最低点到C点的过程,由机械能守恒得
mv2=
m
+mgR(1-cos37°)
在最低点:N-mg=m
解得,N=1.75×103N
(3)由于机械能守恒,则有vB=vC
从A到B,由动能定理得
(mgsin37°-μmgcos37°)L=
m
解得L≈5.56m
答:
(1)小同学登上平台时的速度是5.33m/s;
(2)滑板在圆弧轨道最低点受到轨道的作用力大小是1.75×103N;
(3)A、B两点间的距离是5.56m.
| v | 2 y |
又tan37°=
| vy |
| vx |
解得 vx=
| 16 |
| 3 |
(2)由sin37°=
| vy |
| vC |
| 20 |
| 3 |
从最低点到C点的过程,由机械能守恒得
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 C |
在最低点:N-mg=m
| v2 |
| R |
解得,N=1.75×103N
(3)由于机械能守恒,则有vB=vC
从A到B,由动能定理得
(mgsin37°-μmgcos37°)L=
| 1 |
| 2 |
| v | 2 B |
解得L≈5.56m
答:
(1)小同学登上平台时的速度是5.33m/s;
(2)滑板在圆弧轨道最低点受到轨道的作用力大小是1.75×103N;
(3)A、B两点间的距离是5.56m.
点评:本题主要考查了平抛运动、动能定理及机械能守恒、牛顿运动定律等基本规律的应用,关键是巧用逆向思维求出速度.

练习册系列答案
相关题目
如图所示,某同学设计的“探究加速度与物体所受合力F及质量m的关系”实验装置简图, A为小车,B为电磁打点计时器,C为装有砝码的小桶,D为一端带有定滑轮的长方形木板,在实验中细绳对小车拉力F近似等于砝码和小桶的总重力,小车运动加速度a可用纸带上的点求得

(1)关于该实验,下列说法中不正确的是 ▲ .
A.本实验采用了控制变量的方法进行探究
 B.通过作v-t图像求加速度,可以更好地减小误差
B.通过作v-t图像求加速度,可以更好地减小误差
C.电磁打点计时器使用低压(一般为4—6V)直流电源
D.为减少小车受到的摩擦力对实验的影响,可以把木板D的右端适当垫高
(2)在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别测得小车的加速度a与对应的质量m数据如下表:
|
次数 |
1 |
2 |
3 |
4 |
5 |
|
小车的加速度a/(m·s-2) |
1.25 |
1.00 |
0.80 |
0.50 |
0.40 |
|
小车的质量m/kg |
0.400 |
0.500 |
0.625 |
1.000 |
1.250 |
|
小车质量的倒数m-1/kg-1 |
2.50 |
2.00 |
1.60 |
1.00 |
0.80 |
根据上表数据,为进一步直观反映F不变时 与m的关系,选小车质量的倒数m-1/kg-1为横坐标,小车的加速度a/(m·s-2)为纵坐标建立坐标系,在答卷纸上画出图像
与m的关系,选小车质量的倒数m-1/kg-1为横坐标,小车的加速度a/(m·s-2)为纵坐标建立坐标系,在答卷纸上画出图像
(3)请你根据你所画的图像求出该小车受到的拉力大小F为 ▲ N.



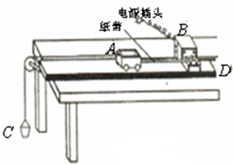 如图所示,某同学设计的“探究加速度与物体所受合力F及质量m的关系”实验装置简图,A为小车,B为电磁打点计时器,C为装有砝码的小桶,D为一端带有定滑轮的长方形木板,在实验中细绳对小车拉力F近似等于砝码和小桶的总重力,小车运动加速度a可用纸带上的点求得
如图所示,某同学设计的“探究加速度与物体所受合力F及质量m的关系”实验装置简图,A为小车,B为电磁打点计时器,C为装有砝码的小桶,D为一端带有定滑轮的长方形木板,在实验中细绳对小车拉力F近似等于砝码和小桶的总重力,小车运动加速度a可用纸带上的点求得