题目内容
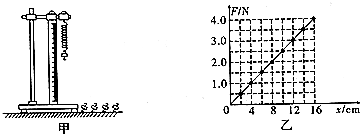
12.如图甲所示,电源由n个电动势E=1.5V、内阻均为r(具体值未知)的电池串联组成,合上开关,在变阻器的滑片C从A端滑到B端的过程中,电路中的一些物理量的变化如图乙中Ⅰ、Ⅱ、Ⅲ所示,电表对电路的影响不计.(Ⅰ图为输出功率与路端电压关系曲线;Ⅱ图为路端电压与总电流关系图线;Ⅲ图为电源的输出效率与外电阻的关系图线)
(1)求组成电源的电池的个数,一个电池的内阻以及变阻器的总阻值.
(2)将Ⅰ、Ⅱ、Ⅲ三个图上的a、b、c各点的坐标求出来.
分析 (1)图中电流表测电路中总电流,电压表测路端电压,即滑动变阻器两端的电压;当滑动变阻器接入电路的阻值为零时,电路短路,电路电流为短路电流,等于电源电压与电源内阻的比值;当滑动变阻器接入电路的阻值与电源内阻阻值相等时,电源输出功率最大,根据图象数据,应用欧姆定律与电功率公式列方程,求出电源电压,然后求出电池节数.电源的输出功率与电源的总功率之比是电源的效率,滑动变阻器接入电路的阻值越大,电源效率越高,当滑动变阻器阻值全部接入电路时,滑动变阻器效率最高,由图丙所示图象,应用电功率公式及效率公式可以求出滑动变阻器的最大阻值.
(2)由欧姆定律、串联电路特点及图象可以求出各点的坐标.
解答 解:(1)设电源的总电动势为E,总内阻为r,据图象的物理意义:由图Ⅰ知,输出的最大电功率 P出m═4.5W
由图Ⅱ可知,短路电流 I短═3A
即得 $\frac{E}{r}$=I短═3A
由于滑动变阻器接入电路的电阻与电源内阻相等,由串联电路特点知,电源内阻电压等于滑动变阻器电压,
则滑动变阻器电压为$\frac{E}{2}$,R滑=r,由乙图得:P最大=$\frac{{U}_{滑}^{2}}{{R}_{滑}}$=$\frac{{E}^{2}}{4r}$=4.5W,
解得:E=6V,r=2Ω,每节干电池的电动势为1.5V,所以电源由4节干电池组成,每个电池的内阻.
r0=$\frac{r}{4}$=$\frac{2}{4}$=0.5Ω
由图Ⅲ可知,当滑片在B端时(即变阻器接入电路的电阻最大时)
η=$\frac{R}{R+r}$×100%=80%
联立解得:变阻器的总阻值 R=8Ω.
(2)由题图Ⅱ求a点的坐标:电路中电流的最小值Ia═0.6A,此时路端电压Ua=IaRm=4.8V,因此,a点坐标为(0.6A,4.8V)
由题图Ⅰ求b、c两点坐标:当输出功率最大时,外电阻等于内阻(R=4r=2Ω),此时Ub=3V,所以b点的坐标为(3V,4.5W)
当C滑到B端时,有:IB═0.6A
PB=UBIB=2.88W
所以c点的坐标为(4.8V,2.88W)
因为Rm=8Ω,所以d点的坐标为(8Ω,80%).
答:
(1)串联干电池的个数为4个,每个电池的内阻为0.5Ω.滑动变阻器的最大阻值为8Ω.
(2)各点坐标分别为:a(0.6A、4.8V);b(3V、4.5W);c(4.8V、2.88W).
点评 本题的关键要分析清楚电路结构,根据各图象获得所需的信息,应用欧姆定律、电功率公式、效率公式等即可正确解题.

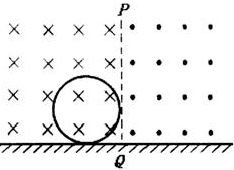 如图所示,在光滑的水平地面卜方,有两个磁感应强度大小均为B,方向向反的水平匀强磁场,PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,从圆环刚好与边界线PQ相切时开始,在外力作用下以速度v向右匀速运动,到圆环运动到直径刚好与边界线PQ重合时,下列说法正确的是( )
如图所示,在光滑的水平地面卜方,有两个磁感应强度大小均为B,方向向反的水平匀强磁场,PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,从圆环刚好与边界线PQ相切时开始,在外力作用下以速度v向右匀速运动,到圆环运动到直径刚好与边界线PQ重合时,下列说法正确的是( )| A. | 此时圆环中的电动势大小为2Bav | |
| B. | 此时圆环中的电流方向为逆时针方向 | |
| C. | 此过程中圆环中的电动势均匀增大 | |
| D. | 此过程中通过圆环截面的电量为$\frac{πB{a}^{2}}{R}$ |
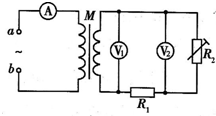 如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )
如图所示,M是一个小型理想变压器,原、副线圈匝数之比n1:n2=10:1,接线柱a、b接电压u=311sin100πt(V)的正弦交变电源.变压器右侧部分为一火警系统原理图,其中R2为用半导体热敏材料制成的传感器(电阻随温度升高而减小),R1为一定值电阻.下列说法正确的是( )| A. | 当R2所在处出现火警时,电阻R1的功率变小 | |
| B. | 当R2所在处出现火警时,电压表V2的示数变小 | |
| C. | 当R2所在处出现火警时,电流表A的示数变小 | |
| D. | 电压表V1示数为22V |
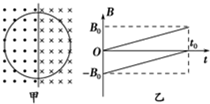 在半径为r.电阻为R的圆形导线框内,以直径为界,左、右两侧分别存在着方向如图甲所示的匀强磁场,以垂直纸面向外的磁场为正,两部分磁场的磁感应强度B随时间t的变化规律分别如图乙所示.则0~t0时间内,导线框中( )
在半径为r.电阻为R的圆形导线框内,以直径为界,左、右两侧分别存在着方向如图甲所示的匀强磁场,以垂直纸面向外的磁场为正,两部分磁场的磁感应强度B随时间t的变化规律分别如图乙所示.则0~t0时间内,导线框中( )| A. | 没有感应电流 | B. | 感应电流方向为顺时针 | ||
| C. | 感应电流大小为$\frac{π{r}^{2}{B}_{0}}{{t}_{0}R}$ | D. | 感应电流大小为$\frac{2π{r}^{2}{B}_{0}}{{t}_{0}R}$ |
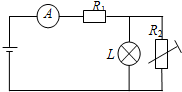
| A. | R1两端的电压变小 | B. | 电流表的示数增大 | ||
| C. | 小灯泡的亮度变小 | D. | 小灯泡的亮度变大 |
| A. | 物体在某时刻的速度为3m/s,则物体在1s内一定走3m | |
| B. | 物体在某1s内的平均速度是3m/s,则物体在这1s内的位移一定是3m | |
| C. | 物体在某段时间内的平均速度是3m/s,则物体在其中某1s内的位移一定是3m | |
| D. | 若物体做匀变速直线运动时,在发生某段位移过程中的平均速度是3m/s,则物体在这段位移的一半时的速度一定是大于3m/s |
| A. | 24 m/s 10 m/s | B. | 24 m/s 8 m/s | C. | 12 m/s 24 m/s | D. | 24 m/s 12 m/s |
 某同学想利用以下器材组装一只欧姆表,并比较精确地测量一只约几千欧电阻的阻值.
某同学想利用以下器材组装一只欧姆表,并比较精确地测量一只约几千欧电阻的阻值.