题目内容
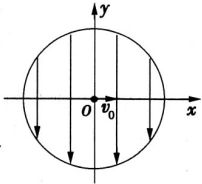 竖直平面xOy内有一半径为R=
竖直平面xOy内有一半径为R=| 2 |
(1)由坐标原点O沿x轴正方向喷出的油滴,在电场中运动的时间;
(2)射出圆形电场油滴的最大动能.
分析:(1)根据牛顿第二定律与运动学公式,即可求解;
(2)根据动能定理,即可求解.
(2)根据动能定理,即可求解.
解答:解:(1)油滴沿x轴方向做匀速运动,速度为v0,沿-y方向做匀加速运动,加速度为a,
则有:mg-qE=ma
y=
at2
解得:t=1s
(2)重力和电场力的合力做功最多的油滴射出圆形电场的动能最大,从喷枪喷出的油滴,沿-y方向射出的油滴有最大动能Ekm
则有:(mg-qE)R=Ekm-
mv02
即,Ekm=
m
+(mg-qE)R
代入数据解得:Ekm=7.8×10-6J
答:
(1)由坐标原点O沿x轴正方向喷出的油滴,在电场中运动的时间1s;
(2)射出圆形电场油滴的最大动能7.8×10-6J.
则有:mg-qE=ma
y=
| 1 |
| 2 |
解得:t=1s
(2)重力和电场力的合力做功最多的油滴射出圆形电场的动能最大,从喷枪喷出的油滴,沿-y方向射出的油滴有最大动能Ekm
则有:(mg-qE)R=Ekm-
| 1 |
| 2 |
即,Ekm=
| 1 |
| 2 |
| v | 2 0 |
代入数据解得:Ekm=7.8×10-6J
答:
(1)由坐标原点O沿x轴正方向喷出的油滴,在电场中运动的时间1s;
(2)射出圆形电场油滴的最大动能7.8×10-6J.
点评:考查牛顿第二定律与运动学公式,及动能定理的掌握与应用.强调对研究对象的受力分析,突出动能定理中的功的正负.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 竖直平面xoy内有一半径为R=
竖直平面xoy内有一半径为R= m,圆心O与坐标系的原点重合的圆形区域,如图所示,在圆心O有一喷枪可在xoy平面内沿各个方向喷出初速度为v=1m/s,质量为m=1×10-6kg,带电量为q=-1×10-8C的油滴.圆形区域内的匀强电场方向沿-y方向,电场强度E=8×102 N/C.(不考虑油滴间的相互作用 )
m,圆心O与坐标系的原点重合的圆形区域,如图所示,在圆心O有一喷枪可在xoy平面内沿各个方向喷出初速度为v=1m/s,质量为m=1×10-6kg,带电量为q=-1×10-8C的油滴.圆形区域内的匀强电场方向沿-y方向,电场强度E=8×102 N/C.(不考虑油滴间的相互作用 ) 竖直平面xoy内有一半径为R=
竖直平面xoy内有一半径为R= m,圆心O与坐标系的原点重合的圆形区域,如图所示,在圆心O有一喷枪可在xoy平面内沿各个方向喷出初速度为v=1m/s,质量为m=1×10-6kg,带电量为q=-1×10-8C的油滴.圆形区域内的匀强电场方向沿-y方向,电场强度E=8×102 N/C.(不考虑油滴间的相互作用 )
m,圆心O与坐标系的原点重合的圆形区域,如图所示,在圆心O有一喷枪可在xoy平面内沿各个方向喷出初速度为v=1m/s,质量为m=1×10-6kg,带电量为q=-1×10-8C的油滴.圆形区域内的匀强电场方向沿-y方向,电场强度E=8×102 N/C.(不考虑油滴间的相互作用 )