题目内容
15. 如图,某同学在地面上拉着一个质量为m=30kg的箱子前进,已知拉力F大小为100$\sqrt{2}$N,与水平面间的夹角为θ=45°,试问:
如图,某同学在地面上拉着一个质量为m=30kg的箱子前进,已知拉力F大小为100$\sqrt{2}$N,与水平面间的夹角为θ=45°,试问:(1)若箱子匀速前进,则箱子受地面的摩擦阻力多大?箱子对地面的压力多大
(2)若撤去拉力后箱子还能滑行0.1m,则箱子匀速运动时的速度多大?
分析 (1)根据水平方向上平衡求出摩擦阻力的大小,根据竖直方向上平衡求出支持力的大小,从而得出箱子对地面的压力大小.
(2)根据滑动摩擦力公式求出动摩擦因数,结合牛顿第二定律求出加速度大小,根据速度位移公式求出匀速运动的速度.
解答 解:(1)箱子匀速前进,在水平方向上有:$f=Fcos45°=100\sqrt{2}×\frac{\sqrt{2}}{2}N=100N$,
在竖直方向上有:N+Fsin45°=mg,
解得支持力N=$mg-Fsin45°=300-100\sqrt{2}×\frac{\sqrt{2}}{2}$=200N.
(2)物体做匀速运动时,动摩擦因数$μ=\frac{f}{N}=\frac{100}{200}=0.5$,
撤去拉力后,箱子的加速度大小a=μg=0.5×10m/s2=5m/s2,
根据v2=2ax得,箱子匀速运动的速度v=$\sqrt{2ax}=\sqrt{2×5×0.1}$m/s=1m/s.
答:(1)箱子受地面的摩擦阻力为100N,箱子对地面的压力为200N;
(2)箱子匀速运动时的速度为1m/s.
点评 本题考查了牛顿第二定律和共点力平衡的基本运用,知道加速度是联系力学和运动学的桥梁,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.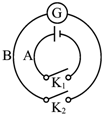 AB两回路中各有一电键K1、K2,且回路A中接有电源,回路B中接有灵敏电流计(如图),下列操作及相应的结果可能实现的是( )
AB两回路中各有一电键K1、K2,且回路A中接有电源,回路B中接有灵敏电流计(如图),下列操作及相应的结果可能实现的是( )
 AB两回路中各有一电键K1、K2,且回路A中接有电源,回路B中接有灵敏电流计(如图),下列操作及相应的结果可能实现的是( )
AB两回路中各有一电键K1、K2,且回路A中接有电源,回路B中接有灵敏电流计(如图),下列操作及相应的结果可能实现的是( )| A. | 先闭合K2,后闭合K1的瞬间,电流计指针偏转 | |
| B. | 先闭合K1,后闭合K2的瞬间,电流计指针偏转 | |
| C. | K1、K2闭合后,在断开K2的瞬间,电流计指针偏转 | |
| D. | K1、K2闭合后,在断开K1的瞬间,电流计指针偏转 |
10.某物体在四个共点力的作用下处于静止状态,若其中F4的方向沿逆时针转90°而保持其大小不变,其余三个力保持不变,则此时物体所受合力大小为( )
| A. | $\sqrt{2}$F4 | B. | 2F4 | C. | F4 | D. | 0 |
20.M、N为电场中的两点,一带正电的点电荷在从M到N的过程中克服电场力做功,设该点电荷仅受电场力作用,则下列说法中一定正确的是( )
| A. | M点电势低于N点电势 | |
| B. | 该电荷在M点的动能大于在N点的动能 | |
| C. | M点场强小于N点场强 | |
| D. | 该点电荷在M点的加速度大于在N点的加速度 |
7.小灯泡灯丝的电阻会随温度的升高而变大.某同学为研究这一现象,用实验得到如下数据(I和U分别表示小灯泡上的电流和电压):
(1)在方框图中画出实验电路原理图.可用的器材有:电压表、电流表、滑动变阻器(0-10Ω)、电源、小灯泡、电键、导线若干.
(2)在图中描出小灯泡的U-I曲线.
(3)现在测得一个电池的电动势是1.5V,内阻是2.0Ω.问:将本试验的小灯泡接在该电池两端,小灯泡的实际功率是0.27W.
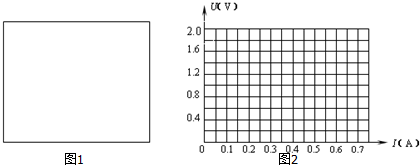
| I(A) | 0.12 | 0.21 | 0.29 | 0.34 | 0.38 | 0.42 | 0.45 | 0.47 | 0.49 | 0.50 |
| U(A) | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
(2)在图中描出小灯泡的U-I曲线.
(3)现在测得一个电池的电动势是1.5V,内阻是2.0Ω.问:将本试验的小灯泡接在该电池两端,小灯泡的实际功率是0.27W.

5.下列说法正确的是( )
| A. | 物体受到的重力是由于地球吸引而产生的 | |
| B. | 重心是重力的作用点,它总是在物体上,不可能在物体外 | |
| C. | 任何几何形状规则的物体,重心必与其几何中心重合 | |
| D. | 重力加速度g是标量,有大小没方向,通常计算中g取9.8m/s2 |
 如图所示,重物2在水平面上保持静止状态,OA绳与水平方向的夹角为60°,OB绳为水平方向,悬挂的物体1重为10N,求:
如图所示,重物2在水平面上保持静止状态,OA绳与水平方向的夹角为60°,OB绳为水平方向,悬挂的物体1重为10N,求: 如图所示,两位同学用弹簧测力计在电梯中做实验.他们先将测力计挂在固定于电梯壁的钩子上,然后将一质量为0.5kg的物体挂在测力计挂钩上.若电梯上升时测力计的示数为6N,则电梯加速度的大小为2m/s2,电梯处于超重状态.(选填“超重”或“失重”).
如图所示,两位同学用弹簧测力计在电梯中做实验.他们先将测力计挂在固定于电梯壁的钩子上,然后将一质量为0.5kg的物体挂在测力计挂钩上.若电梯上升时测力计的示数为6N,则电梯加速度的大小为2m/s2,电梯处于超重状态.(选填“超重”或“失重”). 试判断图中所示的带电粒子刚进入磁场时所受的洛伦兹力的方向.
试判断图中所示的带电粒子刚进入磁场时所受的洛伦兹力的方向.