题目内容
【题目】如图，矩形abcd区域有磁感应强度为B的匀强磁场，ab边长为3L，bc边足够长。厚度不计的挡板MN长为5L，平行bc边放置在磁场中，与bc边相距L，左端与ab边也相距L。质量为m、电荷量为e的电子，由静止开始经电场加速后沿ab边进入磁场区域，电子与挡板碰撞后完全被吸收并导走。
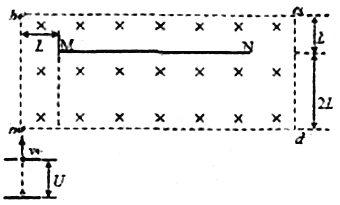
（1）如果加速电压控制在一定范围内，能保证在这个电压范围内加速的电子进入磁场后在磁场中运动时间都相同。求这个加速电压U的范围。
（2）调节加速电压，使电子能落在挡板上表面，求电子落在挡板上表面的最大宽度
【答案】（1）
（2）
【解析】
试题分析：（1）只要电子从ad边离开磁场，其运动的轨迹为半圆，运动时间相同，都为
，当垫子与挡板下表面相切时，轨迹的半径
，圆心为
，如图所示，要使垫子在磁场中的运动时间相等，必须满足：
①
根据牛顿第二定律
②
根据动能定理：
③
联立解得
④（取等号也可）
若垫子恰好能绕过挡板最后段从ad边离开磁场，设其轨迹的半径为
，根据几何关系可得
⑤
解得
⑥，即电子将从bc边出去了，即电子不可能绕过挡板最右端N点从ad边离开磁场，所以，使得电子在磁场中运动时间相同的电压的取值范围是
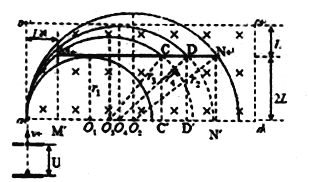
（2）电子能打到挡板上表面必须满足一下要求：
（i）电子能通过M点边缘，设其对应的半径为
，圆心为
，打在上板的C点，
则有：
⑧，
⑨
（ii）电子不能从bc边射出，设电子轨迹与bc边相切时的半径为
，圆心为
，打在上板的D点，则有：
，
所以
练习册系列答案
相关题目
