题目内容
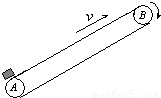
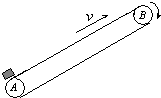 如图为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离l=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.
如图为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离l=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.某同学根据以上条件,提出一种计算时间t的方法:由f-mgsinθ=ma和l=
| 1 | 2 |
请判断上面的解法是否正确,并说明理由.如果正确,请代入数据计算出结果;如不正确,请给出正确的解法和结果.
分析:物块放上传送带先做匀加速直线运动,当物块达到传送带速度时,和传送带一起做匀速直线运动.结合牛顿第二定律和运动学公式求出物体从A处传送到B处所需的时间.
解答:解:上面的解法是错误的,认为物块一直做匀加速直线运动.
正确解法:根据牛顿第二定律得,a=
=
=1m/s2.
当物体速度达到1m/s时的时间t1=
=1s,位移x1=
at12=0.5m.
因为最大静摩擦力大于重力沿斜面方向上的分力,知物块然后做匀速运动.
匀速运动的时间t2=
=
s=3.5s.
则总时间t=t1+t2=4.5s.
答:物体从A处传送到B处所需的时间t为4.5s.
正确解法:根据牛顿第二定律得,a=
| f-mgsinθ |
| m |
| 0.6mg-0.5mg |
| m |
当物体速度达到1m/s时的时间t1=
| v |
| a |
| 1 |
| 2 |
因为最大静摩擦力大于重力沿斜面方向上的分力,知物块然后做匀速运动.
匀速运动的时间t2=
| l-x1 |
| v |
| 4-0.5 |
| 1 |
则总时间t=t1+t2=4.5s.
答:物体从A处传送到B处所需的时间t为4.5s.
点评:解决本题的关键理清物块的运动情况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
 如图所示,ABCD为一倾角θ=30°的粗糙斜面,AD边与BC边平行,有一重力G=10N放在斜面上,当对物体施加一个与AB边平行的拉力F时,物体恰能做匀速直线运动.已知物体与斜面的动摩擦因数μ=
如图所示,ABCD为一倾角θ=30°的粗糙斜面,AD边与BC边平行,有一重力G=10N放在斜面上,当对物体施加一个与AB边平行的拉力F时,物体恰能做匀速直线运动.已知物体与斜面的动摩擦因数μ=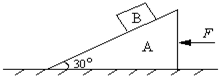 如图,一倾角为30°的直角三角形物块A,质量为m1,在其斜面上放置一质量为m2的物块B,物块与斜面间无摩擦,为了使B相对斜面静止,需A在水平面上向左作匀加速运动.
如图,一倾角为30°的直角三角形物块A,质量为m1,在其斜面上放置一质量为m2的物块B,物块与斜面间无摩擦,为了使B相对斜面静止,需A在水平面上向左作匀加速运动.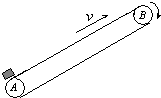 如图为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离l=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.
如图为一倾角θ=30°的传送带装置示意图,绷紧的传送带在A、B间始终保持v=1m/s的恒定速率向上运行,一质量m=2kg的物体无初速地放在A处,传送带就将物体传送上去.设物体与传送带间的滑动摩擦力f=0.6mg,AB间的距离l=4m,g取10m/s2.求物体从A处传送到B处所需的时间t.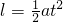 可解得t.
可解得t.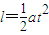 可解得t.
可解得t.