题目内容
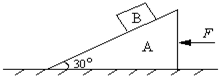如图，一倾角为30°的直角三角形物块A，质量为m1，在其斜面上放置一质量为m2的物块B，物块与斜面间无摩擦，为了使B相对斜面静止，需A在水平面上向左作匀加速运动．（1）求此加速度a的大小；
（2）若A与水平面间动摩擦因数为?，求作用在A的水平外力F的大小．
分析：（1）对物体B受力分析，受重力和支持力，加速度水平向左，故合力水平向左，根据牛顿第二定律列式求解即可；
（2）对整体受力分析，受重力、支持力、摩擦力和推力，根据牛顿第二定律列式求解．
（2）对整体受力分析，受重力、支持力、摩擦力和推力，根据牛顿第二定律列式求解．
解答：解：（1）对B受力分析图如图：
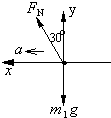
对B：根据牛顿第二定律，有：
y方向：FN?cos30°=m1g…①
x方向：FN?sin30°=m1a …②
由①②得：a=gtan30°=
g …③
（2）A、B加速度相同，相对静止，采用整体法，根据牛顿第二定律，有：
F-μ（m1+m2）g=（m1+m2）a …④
故 F=（m1+m2）（μ+
）g
答：（1）求此加速度a的大小为
g；
（2）作用在A的水平外力F的大小为（m1+m2）（μ+
）g．
对B：根据牛顿第二定律，有：
y方向：FN?cos30°=m1g…①
x方向：FN?sin30°=m1a …②
由①②得：a=gtan30°=
| ||
| 3 |
（2）A、B加速度相同，相对静止，采用整体法，根据牛顿第二定律，有：
F-μ（m1+m2）g=（m1+m2）a …④
故 F=（m1+m2）（μ+
| ||
| 3 |
答：（1）求此加速度a的大小为
| ||
| 3 |
（2）作用在A的水平外力F的大小为（m1+m2）（μ+
| ||
| 3 |
点评：本题关键是明确滑块B和整体的受力情况，然后根据牛顿第二定律列方程求解，不难．
练习册系列答案
星级口算天天练系列答案
相关题目
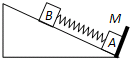如图，一倾角为θ=30°的足够长固定光滑斜面底端有一与斜面垂直的挡板M，物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上．现用外力沿斜面向下缓慢推动物块B，当弹簧具有5J的弹性势能时撤去推力，释放物块B．已知物块A、B的质量分别为5kg和10kg，弹簧的弹性势能的表达式为
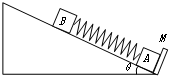如图，一倾角为30°的光滑斜面，底端有一与斜面垂直的固定档板M，物块A、B之间用一与斜面平行轻质弹簧连结，现用力缓慢沿斜面向下推动物块B，当弹簧具有5J弹性势能时撤去推力，释放物块B；已知A、B质量分别为5kg、2kg，弹簧的弹性势能表达式为EP=
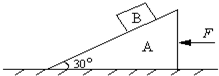如图，一倾角为30°的直角三角形物块A，质量为m1，在其斜面上放置一质量为m2的物块B，物块与斜面间无摩擦，为了使B相对斜面静止，需A在水平面上向左作匀加速运动．
kx2，其中k为弹簧的劲度系数，大小为1 000 N/m，x为弹簧形变量。（g取