题目内容
【题目】如图所示，水平圆盘上沿直径方向放置以轻绳相连的两个小物块A和B。两物块的质量分别为mA和mB，到圆心的距离分别为r和3r。两物块与圆盘间的最大静摩擦力均为自身重力的μ倍，重力加速度为g。不考虑轻绳拉力上限，轻绳伸直且最初拉力为零。圆盘绕过圈心的竖直轴转动，转动的角速度由零缓慢增大，求：
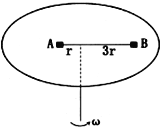
（1）角速度增大至多少时轻绳开始出现拉力?
（2）若mA =mB，角速度在什么范围内，两物块与圆盘之间都不发生相对滑动?
（3）是否存在这种可能性：当两物块的质量满足一定关系，无论角速度多大，两物块与圆盘之间都不发生相对滑动?若不可能请说明原因，若可能请求出需满足的条件。
【答案】
两物块不会与圆盘发生相对滑动
【解析】
解：（1）物块 B 先到达最大静摩擦力，此时绳子开始出现张力
解得
（2）当两物块与圆盘到达最大静摩擦力时，恰好不与圆盘发生相对滑动，物块 A 的摩擦力延半径向外
所以
（3）有可能
联立解得
若满足：mA =3mB ，物块A的摩擦力总满足 f A=μmBg<μmAg
无论角速度多大，两物块不会与圆盘发生相对滑动
练习册系列答案
相关题目
