题目内容
(13分)如图所示,在两条平行的虚线内存在着宽度为L、场强为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏。现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O。试求: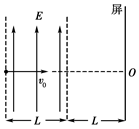
(1)粒子从射入到打到屏上所用的时间;
(2)粒子打到屏上的点P到O点的距离;
(3)粒子在整个运动过程中动能的变化量。
(1) 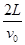 (2)
(2) 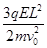 (3)
(3) 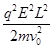
解析试题分析:(1)根据题意,粒子在垂直于电场线的方向上做匀速直线运动,所以粒子从射入到打到屏上所用的时间t=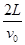 3分
3分
(2)设粒子射出电场时沿平行电场线方向的速度为vy,
根据牛顿第二定律,粒子在电场中的加速度为:a=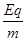 1分
1分
所以vy=a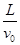 =
=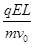 1分
1分
所以粒子刚射出电场时的速度方向与初速度方向间夹角的正切值为:
tan α=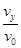 =
=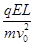 . 1分
. 1分
设粒子在电场中的偏转距离为y,则 y=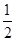 a
a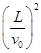 =
=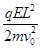 2分
2分
又s=y+Ltanα,解得:s=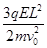 2分
2分
(3)整个运动过程只有电场力做功,根据动能定理:△EK=qEy=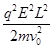 3分
3分
考点:本题考查带电粒子的运动、运动的分解、动能定理,意在考查学生的综合分析能力。

练习册系列答案
相关题目


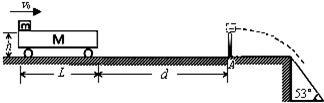

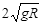 。求:
。求:
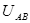 ;
;

 。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3,如图所示。空气和桌面对物体的阻力均忽略不计。
。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3,如图所示。空气和桌面对物体的阻力均忽略不计。
