题目内容
 (2008?广州模拟)如图所示,一轻绳上端系在车的左上角的A点,另一轻绳一端系在车左端B点,B点在A点正下方,A、B距离为b,两绳另一端在C点相结并系一质量为m的小球,绳AC长度为
(2008?广州模拟)如图所示,一轻绳上端系在车的左上角的A点,另一轻绳一端系在车左端B点,B点在A点正下方,A、B距离为b,两绳另一端在C点相结并系一质量为m的小球,绳AC长度为| 2 |
(1)绳BC刚好被拉直时,车的加速度是多大?(要求画出受力图)
(2)在不拉断轻绳的前提下,求车向左运动的最大加速度是多大?(要求画出受力图)
分析:(1)绳BC刚好被拉直时,拉力仍为零,小球受到AC绳的拉力和重力作用,根据牛顿第二定律求解球的加速度,即为车的加速度.
(2)小车向左的加速度增大,AB、BC绳方向不变,所以AC绳拉力不变,BC绳拉力变大,BC绳拉力最大时,小车向左的加速度最大,根据牛顿第二定律求出车向左运动的最大加速度.
(2)小车向左的加速度增大,AB、BC绳方向不变,所以AC绳拉力不变,BC绳拉力变大,BC绳拉力最大时,小车向左的加速度最大,根据牛顿第二定律求出车向左运动的最大加速度.
解答: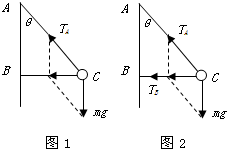 解:(1)绳BC刚好被拉直时,小球受力如图1所示
解:(1)绳BC刚好被拉直时,小球受力如图1所示
因为 AB=BC=b,AC=
b
故绳BC方向与AB垂直,cosθ=
得θ=45°
由牛顿第二定律,得 mgtanθ=ma
可得 a=g
(2)小车向左的加速度增大,AB、BC绳方向不变,所以AC绳拉力不变,BC绳拉力变大,BC绳拉力最大时,小车向左的加速度最大,小球受力如图2所示.由牛顿第二定律,得
Tm+mgtanθ=mam
因这时 Tm=2mg
所以最大加速度为 am=3g
答:
(1)绳BC刚好被拉直时,车的加速度是g.
(2)在不拉断轻绳的前提下,车向左运动的最大加速度是3g.
 解:(1)绳BC刚好被拉直时,小球受力如图1所示
解:(1)绳BC刚好被拉直时,小球受力如图1所示因为 AB=BC=b,AC=
| 2 |
故绳BC方向与AB垂直,cosθ=
| ||
| 2 |
由牛顿第二定律,得 mgtanθ=ma
可得 a=g
(2)小车向左的加速度增大,AB、BC绳方向不变,所以AC绳拉力不变,BC绳拉力变大,BC绳拉力最大时,小车向左的加速度最大,小球受力如图2所示.由牛顿第二定律,得
Tm+mgtanθ=mam
因这时 Tm=2mg
所以最大加速度为 am=3g
答:
(1)绳BC刚好被拉直时,车的加速度是g.
(2)在不拉断轻绳的前提下,车向左运动的最大加速度是3g.
点评:本题属于已知受力情况确定运动情况的类型,根据牛顿第二定律进行研究,作出力图是解答的基础.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 (2008?广州模拟)如图所示,从点光源S发出的一细束白光以一定的角度入射到三棱镜的表面,经过三棱镜的折射后发生色散现象,在光屏的ab间形成一条彩色光带.下面的说法中正确的是( )
(2008?广州模拟)如图所示,从点光源S发出的一细束白光以一定的角度入射到三棱镜的表面,经过三棱镜的折射后发生色散现象,在光屏的ab间形成一条彩色光带.下面的说法中正确的是( ) (2008?广州模拟)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB和着陆雪道CD,以及水平的起跳平台BC组成,AB与BC圆滑连接.运动员从助滑雪道AB上由静止开始下滑,到达C点后水平飞出,以后落到F点.E是运动轨迹上的某一点,在该点运动员的速度方向与轨道CD平行.设运动员从C到E与从E与F的运动时间分别为tCE和tEF,则它们的大小关系为( )
(2008?广州模拟)如图是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB和着陆雪道CD,以及水平的起跳平台BC组成,AB与BC圆滑连接.运动员从助滑雪道AB上由静止开始下滑,到达C点后水平飞出,以后落到F点.E是运动轨迹上的某一点,在该点运动员的速度方向与轨道CD平行.设运动员从C到E与从E与F的运动时间分别为tCE和tEF,则它们的大小关系为( )