Question

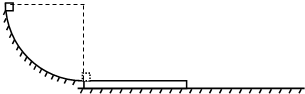
如图所示，半径为R的

1

4

光滑圆弧轨道竖直放置，下端恰与金属板上表面平滑连接．金属板置于水平地面上，板足够长，质量为5m，均匀带正电q；现有一质量为m的绝缘小滑块（可视为质点），由轨道顶端无初速释放，滑过圆弧轨道后滑到金属板上．空间存在竖直向上的匀强电场，场强E=

6mg

q

；已知滑块与金属板上表面、金属板与地面间的动摩擦因数均为μ；重力加速度为g．试求：

（1）滑块滑到圆弧轨道末端时的速度v₀；
（2）金属板在水平地面上滑行的最终速度v；
（3）若从滑块滑上金属板时开始计时，电场存在的时间为t，求电场消失后，金属板在地面上滑行的距离s与t的关系．

Answer 1

（1）滑块滑到轨道末端，有mgR=

1

2

m

v

20

可得，滑块速度为 v₀=

2gR

（2）滑块滑上金属板瞬间，金属板竖直上受力 F=qE=6mg=（m+5m）g，可知板不受地面摩擦力，滑块与金属板组成的系统动量守恒．
mv₀=（m+5m）v
可得金属板在水平地面上滑行的最终速度为v=

1

6

v₀=

2gR

6

（3）设ts末滑块与金属板恰好共速，则对滑块，有
v-v₀=at
又-μmg=ma
可得运动时间t=

5 2gR

6μg

①当t≥

5 2gR

6μg

时，滑块和金属板一起向右匀减速运动至静止，有
-μ（m+5m）gs=0-

1

2

（m+5m）v²
则可得金属板滑行距离s=

R

36μ

②当0＜t＜

5 2gR

6μg

时，电场消失时，滑块与金属板未共速，则此时对金属板有
v′=

μmg

5m

t=

μg

5

t
ts后电场消失，金属板水平方向上受力减速-μ（m+5m）g+μmg=5ma′，得：a′=-μg，
又滑块此时速度大于板，加速度则与板相同．可知板先减速至速度为0后静止
对金属板，有2a′s=0-v′²
可得金属板滑行距离s=

μg

50

t2
综上所述，当0＜t＜

5 2gR

6μg

时，电场消失后金属板滑行距离s=

μg

50

t2；
当t≥

5 2gR

6μg

时，电场消失后金属板滑行距离s=

R

36μ

答：
（1）滑块滑到圆弧轨道末端时的速度v₀为

2gR

．
（2）金属板在水平地面上滑行的最终速度v为

2gR

6

；
（3）电场消失后，金属板在地面上滑行的距离s与t的关系为当0＜t＜

5 2gR

6μg

时，电场消失后金属板滑行距离s=

μg

50

t2；当t≥

5 2gR

6μg

时，电场消失后金属板滑行距离s=

R

36μ

．