题目内容
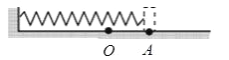
【题目】轻质弹簧一端固定，另一端与放置于水平桌面上的小物块（可视为质点）相连接。弹簧处于原长时物块位于O点。现将小物块向右拉至A点后由静止释放，小物块将沿水平桌面运动。已知弹簧劲度系数为k，小物块质量为m，OA间距离为L，弹簧弹性势能的表达式为
，式中x为弹簧形变量的大小。
(1)若小物块与水平桌面间的动摩擦因数
，且最大静摩擦力等于滑动摩擦力。 求①小物块第一次经过O点时的速度大小；
②小物块向左运动过程中距离O点的最远距离以及最终静止时的位置。
(2)在我们的生活中常常用到弹簧，有的弹簧很“硬”，有的弹簧很“软”，弹簧的“软硬”程度其实是由弹簧的劲度系数决定的。请你自行选择实验器材设计一个测量弹簧劲度系数的实验，简要说明实验方案及实验原理。
【答案】(1)
0.2L(2) 将弹簧竖直悬挂，弹簧下端挂质量不同的物体，稳定后测量弹簧伸长量及弹簧所受拉力，根据胡克定律可得到弹簧的劲度系数。
【解析】
设小物块第一次经过O点时的速度为v，根据功能关系求解速度；设小物块向左运动得最远处在O点左侧的B点，小物块由A运动到B的过程中，由功能关系求出最远距离，再分析B位置受到的弹力与最大静摩擦力的关系，从而判断物块能否静止在B点，若不能静止，再根据功能关系求解即可；将弹簧悬挂，弹簧下端挂质量不同的物体，稳定后测量弹簧伸长量以及弹簧所受的拉力，再根据胡克定律得到弹簧的劲度系数；
解：(1)①设小物块第一次经过O点时的速度为v，根据功能关系得：
解得：
②设小物块向左运动得最远处在O点左侧的B点,BO之间的距离为xB，小物块由A运动到B的过程中，由功能关系得：
解得：
此时弹簧弹力为：
小物块与地面的最大静摩擦力为：
因此小物块不能停在B点，将继续向右运动，设小物块能静止在O点右侧得C点，C与O的距离为xC，小物块由B点运动到C点的过程中，根据功能关系得：
解得：
，则小物块到达B点后向右运动，再次经过O点，最终静止在O点右侧0.2L处。
(2) 方案一：将弹簧竖直悬挂，弹簧下端挂质量不同的物体，稳定后测量弹簧伸长量及弹簧所受拉力，根据胡克定律可得到弹簧的劲度系数。
方案二：将弹簧竖直放置，在弹簧上放置质量不同的物体，稳定后测量弹簧压缩量及弹簧所受压力，根据胡克定律可得到弹簧的劲度系数。
方案三：将弹簧一端固定在水平气垫导轨上，另一端与小滑块相连接，使小滑块在气垫导轨上沿水平方向上做简谐运动，测出小滑块加速度，根据简谐运动特点及牛顿运动定律
可得到弹簧的劲度系数。
