Question

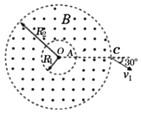
【题目】如图所示，在以O为圆心，内外半径分别为R1=0.5m和R2=1.5m的圆环区域内存在垂直纸面向外的匀强磁场。一电荷量为q、质量为m的粒子从内圆上的A点射入该圆环区域，不计空气阻力及粒子重力。求：

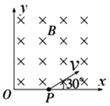
（1）若磁感应强度B=1T，粒子从OA延长线与外圆的交点C以速度v1=105m/s射出，方向与OA延长线成30°角，粒子的电性及比荷；

（2）若粒子仍从A点沿不同方向射入磁场，速度大小为v2=106m/s，要使所有粒子一定都能够从外圆射出，磁感应强度的大小B′满足的条件。

Answer 1

【答案】（1）正电， 105C/kg（2）B′＜10T

【解析】

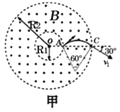
（1）由左手定则知，粒子带正电，粒子的运动轨迹如图甲所示，设粒子运动的轨道半径为r，

由牛顿第二定律得：

又由几何关系可知，粒子运动的半径

r=R2﹣R1=1m

联立解得比荷

（2）要使所有粒子一定都能够从外圆射出，作出粒子刚好与边界相切的两轨迹，如图所示，

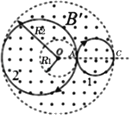
粒子能从轨迹2能射出，则所有粒子一定能从外圆射出，即满足

2r′＞R1+R2

由牛顿第二定律得：

解得：

B′＜10T。