��Ŀ����
7�� 1995��������̫��ϵ�����״η����ƺ��ǹ�ת�����ǣ��˺�����̷�����һ����ʮ�����̫��ϵ��������ǣ�������Щ��̫��ϵ��������ǵ�ԭ����������Ϊ������ΪM�ĺ���������Ϊm�����ǣ�M��m��������֮��������������������й�����˶��ţ���ͼ��ʾ��ʾ������Ϊ��������ijһ����CΪ���ġ��뾶Ϊa��Բ����������Բ���˶���ͼ��û�б�ʾ�����ǣ���������������ΪG�������Լ����ǵĴ�С���Բ��ƣ�������˵����ȷ���ǣ�������
1995��������̫��ϵ�����״η����ƺ��ǹ�ת�����ǣ��˺�����̷�����һ����ʮ�����̫��ϵ��������ǣ�������Щ��̫��ϵ��������ǵ�ԭ����������Ϊ������ΪM�ĺ���������Ϊm�����ǣ�M��m��������֮��������������������й�����˶��ţ���ͼ��ʾ��ʾ������Ϊ��������ijһ����CΪ���ġ��뾶Ϊa��Բ����������Բ���˶���ͼ��û�б�ʾ�����ǣ���������������ΪG�������Լ����ǵĴ�С���Բ��ƣ�������˵����ȷ���ǣ�������| A�� | ���Ǻͺ������е���������С��ͬ�����ٶ���ͬ | |
| B�� | ���Ǻ�C��֮��ľ���b=$\frac{Ma}{m}$ | |
| C�� | ���ǵ���������v=$\frac{M��\frac{GM}{a}��^{\frac{1}{2}}}{M+m}$ | |
| D�� | ���ǵ���������V=$\frac{m��\frac{GM}{a}��^{\frac{1}{2}}}{M+m}$ |
���� ����������Χ�����������ϵ�ijһ�̶���ֱ�������Բ���˶����֮������������ṩ���Ե�������������������ͬ�Ľ��ٶȺ����ڣ�����ţ�ٵڶ����ɷֱ�����ǽ�����ʽ������⣮��������������������������ţ�ٵڶ�������ʽ�����ǵ���������v��
��� �⣺A������ΪM�ĺ���������Ϊm�����ǣ�M��m��������֮�������������������������Բ���˶����֮������������ṩ���Ե�������������ٶ���ͬ����A��ȷ��
B��������m��F=m��2a����
�Ժ���M��F��=M��2b����
�ɵ�b=$\frac{m}{M}a$����B���� 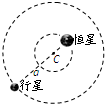 C�������˶��Ĺ����λ�ô�����ͼ���Ժ���M�������������ṩ���������У�
C�������˶��Ĺ����λ�ô�����ͼ���Ժ���M�������������ṩ���������У�
$\frac{GMm}{��a+b��^{2}}=M\frac{{v}^{2}}{b}$
���v=$\frac{m{��\frac{GM}{a}��}^{\frac{1}{2}}}{M+m}$����C����D��ȷ��
��ѡ��AD
���� ������˫�����⣬�ؼ�ץס���㣺һ��˫�����������������ṩ��������˫�ǵ������ǣ����ٶȻ�������ȣ�

��ϰ��ϵ�д�
�����Ŀ
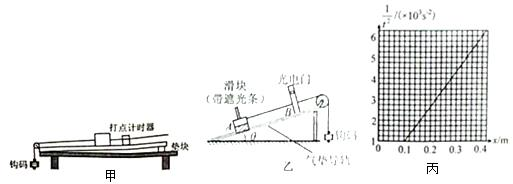
17�� һ����Ϊm��������ˮƽ����F����������ˮƽ���˶�����t0ʱ�̳�ȥ��F����v-tͼ����ͼ��ʾ����֪������ˮƽ���Ķ�Ħ������Ϊ�̣������й�����F�Ĵ�С����F���Ĺ�W�Ĵ�С��ϵʽ��ȷ���ǣ�������
һ����Ϊm��������ˮƽ����F����������ˮƽ���˶�����t0ʱ�̳�ȥ��F����v-tͼ����ͼ��ʾ����֪������ˮƽ���Ķ�Ħ������Ϊ�̣������й�����F�Ĵ�С����F���Ĺ�W�Ĵ�С��ϵʽ��ȷ���ǣ�������
 һ����Ϊm��������ˮƽ����F����������ˮƽ���˶�����t0ʱ�̳�ȥ��F����v-tͼ����ͼ��ʾ����֪������ˮƽ���Ķ�Ħ������Ϊ�̣������й�����F�Ĵ�С����F���Ĺ�W�Ĵ�С��ϵʽ��ȷ���ǣ�������
һ����Ϊm��������ˮƽ����F����������ˮƽ���˶�����t0ʱ�̳�ȥ��F����v-tͼ����ͼ��ʾ����֪������ˮƽ���Ķ�Ħ������Ϊ�̣������й�����F�Ĵ�С����F���Ĺ�W�Ĵ�С��ϵʽ��ȷ���ǣ�������| A�� | F=��mg | B�� | F=2��mg | C�� | W=$\frac{3}{4}$mv02 | D�� | W=$\frac{3}{2}$��mgv0t0 |
15�� ��ͼ��ʾ��M��N��ƽ�а���������������壬R0Ϊ��ֵ���裬R1��R2Ϊ�ɵ����裬�þ�Եϸ�߽�����Ϊm���������С�����ڵ������ڲ����պϵ��S��С��ֹʱ�ܵ����ߵ�����ΪF������R1��R2������F�Ĵ�С�ж���ȷ���ǣ�������
��ͼ��ʾ��M��N��ƽ�а���������������壬R0Ϊ��ֵ���裬R1��R2Ϊ�ɵ����裬�þ�Եϸ�߽�����Ϊm���������С�����ڵ������ڲ����պϵ��S��С��ֹʱ�ܵ����ߵ�����ΪF������R1��R2������F�Ĵ�С�ж���ȷ���ǣ�������
 ��ͼ��ʾ��M��N��ƽ�а���������������壬R0Ϊ��ֵ���裬R1��R2Ϊ�ɵ����裬�þ�Եϸ�߽�����Ϊm���������С�����ڵ������ڲ����պϵ��S��С��ֹʱ�ܵ����ߵ�����ΪF������R1��R2������F�Ĵ�С�ж���ȷ���ǣ�������
��ͼ��ʾ��M��N��ƽ�а���������������壬R0Ϊ��ֵ���裬R1��R2Ϊ�ɵ����裬�þ�Եϸ�߽�����Ϊm���������С�����ڵ������ڲ����պϵ��S��С��ֹʱ�ܵ����ߵ�����ΪF������R1��R2������F�Ĵ�С�ж���ȷ���ǣ�������| A�� | ����R1���䣬��������R2ʱ��F����С | |
| B�� | ����R1���䣬��������R2ʱ��F������ | |
| C�� | ����R2���䣬��������R1ʱ��F����С | |
| D�� | ����R2���䣬��������R1ʱ��F������ |
12����ͼ��ʾ���⻬��ˮƽ��������20��ľ��1��2��3����20����1��3��5����������Ϊm����2��4��6����������Ϊ2m��������F�����Ƶ�һ��ľ�飬���15��ľ��Ե�14��ľ��ĵ�����СΪ��������

| A�� | $\frac{3}{10}$F������ | B�� | $\frac{3}{7}$F������ | C�� | $\frac{4}{15}$F������ | D�� | $\frac{7}{30}$F������ |
16�� 2011��11��8�գ��ҹ���һ������̽������ө��1�š��������˹�IJ�������̽����һ�������գ�������ǣ���ʼ�Ի��ǵ�̽���о����ҹ��Ի��ǵ�̽�⽫��Ϊ�����Σ������Ա̤�ϻ��ǣ����轫���ҹ�һ�ҷɴ��ӻ��Ƿ��ص���ʱ��������ͼ��ʾ�ı����̣�������˵����ȷ���ǣ�������
2011��11��8�գ��ҹ���һ������̽������ө��1�š��������˹�IJ�������̽����һ�������գ�������ǣ���ʼ�Ի��ǵ�̽���о����ҹ��Ի��ǵ�̽�⽫��Ϊ�����Σ������Ա̤�ϻ��ǣ����轫���ҹ�һ�ҷɴ��ӻ��Ƿ��ص���ʱ��������ͼ��ʾ�ı����̣�������˵����ȷ���ǣ�������
 2011��11��8�գ��ҹ���һ������̽������ө��1�š��������˹�IJ�������̽����һ�������գ�������ǣ���ʼ�Ի��ǵ�̽���о����ҹ��Ի��ǵ�̽�⽫��Ϊ�����Σ������Ա̤�ϻ��ǣ����轫���ҹ�һ�ҷɴ��ӻ��Ƿ��ص���ʱ��������ͼ��ʾ�ı����̣�������˵����ȷ���ǣ�������
2011��11��8�գ��ҹ���һ������̽������ө��1�š��������˹�IJ�������̽����һ�������գ�������ǣ���ʼ�Ի��ǵ�̽���о����ҹ��Ի��ǵ�̽�⽫��Ϊ�����Σ������Ա̤�ϻ��ǣ����轫���ҹ�һ�ҷɴ��ӻ��Ƿ��ص���ʱ��������ͼ��ʾ�ı����̣�������˵����ȷ���ǣ�������| A�� | �ɴ��ڹ�������˶�ʱ����P����ٶȴ�����Q����ٶ� | |
| B�� | �ɴ��ڹ�������˶��Ļ�е�ܴ����ڹ�������˶��Ļ�е�� | |
| C�� | �ɴ��ڹ�������˶���P��ʱ�ļ��ٶȵ��ڷɴ��ڹ�������˶���P��ʱ�ļ��ٶ� | |
| D�� | �ɴ��ƻ����ڹ�������˶������ڸ��ɴ����ص���Ĺ������Ƶ����Թ��Iͬ���İ뾶�˶���������ͬ |
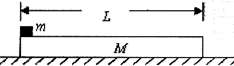 ��ͼ��ʾ������M=1kg��ľ�徲ֹ�ڴֲڵ�ˮƽ�����ϣ�ľ��������Ķ�Ħ������?1=0.1����ľ�����˷���һ������m=1kg����С���Ժ��Ե����飬������ľ���Ķ�Ħ������?2=0.4��ȡg=l0m/s2���������ϼ�һ��ˮƽ���ҵĺ���F=8N��ľ���ڵ��������һ�����ͬʱ��������ľ����Ҳ���ľ�����һ���������
��ͼ��ʾ������M=1kg��ľ�徲ֹ�ڴֲڵ�ˮƽ�����ϣ�ľ��������Ķ�Ħ������?1=0.1����ľ�����˷���һ������m=1kg����С���Ժ��Ե����飬������ľ���Ķ�Ħ������?2=0.4��ȡg=l0m/s2���������ϼ�һ��ˮƽ���ҵĺ���F=8N��ľ���ڵ��������һ�����ͬʱ��������ľ����Ҳ���ľ�����һ���������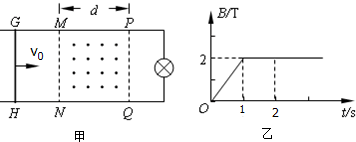 һƽ�н�������ˮƽ���ڹ̶���������L=0.5m�������Ҷ˽��е���R1=4��С���ݣ�������費�ƣ���ͼ�ף��ڵ����MNQP��������������ֱ���ϵĴų���MN��PQ���d=3m��������Ÿ�Ӧǿ��B��ʱ��t�仯������ͼ����ʾ����ֱ������һ����m=1kg�����ˣ������r=1�����������뵼���Ķ�Ħ������Ϊ��=0.2����t=0ʱ�̣������������ٶ�v0=2m/s��ͬʱʩ��һ���ҵ�����F��ʹ���GH�������˶�����0-2s��С�Ʒ�������ʼ��û�仯����
һƽ�н�������ˮƽ���ڹ̶���������L=0.5m�������Ҷ˽��е���R1=4��С���ݣ�������費�ƣ���ͼ�ף��ڵ����MNQP��������������ֱ���ϵĴų���MN��PQ���d=3m��������Ÿ�Ӧǿ��B��ʱ��t�仯������ͼ����ʾ����ֱ������һ����m=1kg�����ˣ������r=1�����������뵼���Ķ�Ħ������Ϊ��=0.2����t=0ʱ�̣������������ٶ�v0=2m/s��ͬʱʩ��һ���ҵ�����F��ʹ���GH�������˶�����0-2s��С�Ʒ�������ʼ��û�仯����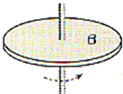 ��ͼ��ʾ��һ��Բ���Ϸ���С��飬��ˮƽ��������ת����ת��������С�����Բ����Ծ�ֹ���ס��������в�ͬ�����������Ϊ������������Բ�̶�����ľ�Ħ������ָ��Բ�ģ�����Ϊ��������ǰ�˶������ƣ���Ħ�������������˶����Ʒ����෴����������Ǻ��˶�����ֱ������������������Ǿ�Ħ��������ͬ��˭�������Ϊʲô��
��ͼ��ʾ��һ��Բ���Ϸ���С��飬��ˮƽ��������ת����ת��������С�����Բ����Ծ�ֹ���ס��������в�ͬ�����������Ϊ������������Բ�̶�����ľ�Ħ������ָ��Բ�ģ�����Ϊ��������ǰ�˶������ƣ���Ħ�������������˶����Ʒ����෴����������Ǻ��˶�����ֱ������������������Ǿ�Ħ��������ͬ��˭�������Ϊʲô��