题目内容

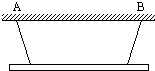如图所示，质量为4kg的均匀杆对称地用两根等长的轻绳悬挂于天花板上A、B两点，绳子与天花板的夹角都为θ=53°，则每根绳子的拉力大小为N，若不改变其他条件，要使每根绳子所受拉力减小些，应将AB间距离（填“增大”或“减小”）些．

25 减小
分析：对物体受力分析：重力和两个拉力，根据平衡条件并结合正交分解法列式求解．
解答：对物体受力分析，受重力和两个拉力，
根据平衡条件，有
T₁cosθ=T₂cosθ ①
T₁sinθ+T₂sinθ=mg ②
解得T₁=T₂=25N
由②得：T₁=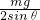 $\text{[math]}$
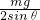
则知要使每根绳子所受拉力减小，必须增大θ，应将AB间距离减小．
故答案为：25，减小
点评：本题关键是对物体受力分析，然后根据平衡条件并结合正交分解法列式求解．

练习册系列答案

超能学典单元期中期末专题冲刺100分系列答案

期末100分冲刺卷系列答案

黄冈360度定制密卷系列答案

①在“利用打点计时器测速度”的实验中，运用

法，可以利用打点计时器打出的纸带测算出某点的瞬时速度：在“探究互成角度的两个力的合成”的实验中，分别用一个力F或两个互成角度的F₁、F₂，把一个一端固定的橡皮筋拉伸到同一位置，则F就是F₁和F₂的合力，实验原理采用的是

法．在“探究平抛运动的规律”的实验中，如图1所示，用小锤打击弹性金属片，金属片把A球沿水平方向抛出，同时B球松开，自由下落，A、B两球同时开始运动，观察到两球同时落地．运用

法，可以判定平抛运动在竖直方向上的分运动是自由落体运动．
②图象法是物理实验中一种重要的研究方法．在研究加速度与外力（质量m一定）的关系、验证机械能守恒定律、探究弹
力大小与弹簧伸长量之间的关系三个实验中，某同学正确作出了三个实验的相关图象，如图2中A、B、C所示．根据坐标轴代表的物理量判断，A实验的图象“斜率”表示

；B实验图象的“斜率”表示

；C实验图象的“斜率”表示

．
（2）某一小型电风扇额定电压为4.0V，额定功率为2.4W．某实验小组想通过实验描绘出小电风扇的伏安特性曲线．实验中除导线和开关外，还有以下器材可供选择：
A．电源E（电动势为4.5V）
B．电压表V（量程为0～5V，内阻约为4kΩ）
C．电流表A₁（量程为0～0.6A，内阻约为0.2Ω）
D．电流表A₂（量程3A，内阻约0.05Ω）；
E．滑动变阻器R₁（最大阻值10Ω，额定电流1A）
F．滑动变阻器R₂（最大阻值2kΩ，额定电流100mA）
①为了便于调节，减小读数误差和系统误差，实验中所用电流表应选用

，滑动变阻器应选用

．（填所选仪器前的字母序号）．
②请你为该小组设计实验电路，并把电路图画在虚线内（小电风扇的电路符号如图3所示）．
③操作过程中发现，小电风扇通电后受阻力作用，电压表读数小于0.5V时电风扇没启动．该小组测绘出的小电风扇的伏安特性曲线如图4所示，由此可以判定，小电风扇的电阻为

同学．
②如图甲所示的装置测定弹簧的劲度系数，被测弹簧一端固定于A点，另一端B用细绳绕过定滑轮悬挂钩码，旁边竖直固定一最小刻度为mm的刻度尺，当挂两个钩码时，绳上一定点P对应刻度如图乙ab虚线所示，再增加一个钩码后，P点对应刻度如图乙cd虚线所示，已知每个钩码质量为50g，重力加速度g=9.80m/s²，则被测弹簧的劲度系数为

N/m，挂三个钩码时弹簧的形变量为

2.10

cm．

（2）为了确定一卷金属漆包线的长度，可通过测定其电阻值和去掉漆层后金属导线的直径来实现．现仅有下列器材：
A、待测漆包线：电阻值R_L在40～50Ω之间，其材料的电阻率ρ=1.7×10^-8Ω?m；
B、毫安表mA：量程1mA，内阻R_A=50Ω； C、电压表V：量程6V，内阻R_V=4kΩ；
D、电源E：电动势约9V，内阻不计； E、滑动变阻器R：阻值范围0～10Ω；
F、螺旋测微器，开关S，导线若干．
①若这卷漆包线的电阻值为R_L，金属导线的直径为d，金属电阻率为ρ，则这卷漆包线的长度L=

（用R_L、d、ρ表示）．
②为了尽可能准确地测定R_L，要求两电表指针偏转至少达到满刻度的一半．同学们设计了以下四种不同的电路，其中合理的是

．

③实验中测得d=0.200mm，按合理的接法测量时，毫安表和电压表的示数如图丙所示，则毫安表的读数为

（13分）（1）在物理实验中体现了很多的物理研究方法，如理想实验法、控制变量法、极限思维法、图像法、类比法、科学假说法、微小量放大法与等效替代法等。请把合适的方法或正确的答案填在相应的空格内。

①在“利用打点计时器测速度”的实验中，运用法，可以利用打点计时器打出的纸带测算出某点的瞬时速度：在“探究互成角度的两个力的合成”的实验中，分别用一个力F或两个互成角度的F₁、F₂，把一个一端固定的橡皮筋拉伸到同一位置，则F就是F₁和F₂的合力，实验原理采用的是法。在“探究平抛运动的规律”的实验中，如图所示，用小锤打击弹性金属片，金属片把A球沿水平方向抛出，同时B球松开，自由下落，A、B两球同时开始运动，观察到两球同时落地。运用法，可以判定平抛运动在竖直方向上的分运动是自由落体运动。

②图象法是物理实验中一种重要的研究方法。在研究加速度与外力（质量m一定）的关系、验证机械能守恒定律、探究弹力大小与弹簧伸长量之间的关系三个实验中，某同学正确作出了三个实验的相关图象，如图中A、B、C所示。根据坐标轴代表的物理量判断，A实验的图象“斜率”表示；B实验图象的“斜率”表示；C实验图象的“斜率”表示。

（2）某一小型电风扇额定电压为4.0V，额定功率为2.4W。某实验小组想通过实验描绘出小电风扇的伏安特性曲线。实验中除导线和开关外，还有以下器材可供选择：

A．电源E（电动势为4.5V）

B．电压表V（量程为0～5V，内阻约为4k）

C．电流表A₁（量程为0～0.6A，内阻约为0.2）

D．电流表A₂(量程3A，内阻约0.05);

E．滑动变阻器R₁（最大阻值10,额定电流1A）

F．滑动变阻器R₂（最大阻值2k,额定电流100mA）

①为了便于调节，减小读数误差和系统误差，实验中所用电流表应选用，滑动变阻器应选用。（填所选仪器前的字母序号）。

②请你为该小组设计实验电路，并把电路图画在虚线内（小电风扇的电路符号如图所示）。

③操作过程中发现，小电风扇通电后受阻力作用，电压表读数小于0.5V时电风扇没启动。该小组测绘出的小电风扇的伏安特性曲线如图所示，由此可以判定，小电风扇的电阻为，正常工作时的发热功率为，机械功率为。

（1）①甲、乙、丙、丁四位同学在使用不同精度的游标卡尺和螺旋测微器测量物体的长度时，分别测量的结果如下：
甲同学：使用游标为50分度的卡尺，读数为12.045cm
乙同学：使用游标为10分度的卡尺，读数为12.04cm
丙同学：使用游标为20分度的卡尺，读数为12.045cm
丁同学：使用精度为“0.01mm”的螺旋测微器，读数为12.040mm
从这些实验数据中可以看出读数肯定有错误的是______同学．
②如图甲所示的装置测定弹簧的劲度系数，被测弹簧一端固定于A点，另一端B用细绳绕过定滑轮悬挂钩码，旁边竖直固定一最小刻度为mm的刻度尺，当挂两个钩码时，绳上一定点P对应刻度如图乙ab虚线所示，再增加一个钩码后，P点对应刻度如图乙cd虚线所示，已知每个钩码质量为50g，重力加速度g=9.80m/s²，则被测弹簧的劲度系数为______N/m，挂三个钩码时弹簧的形变量为______cm．

③实验中测得d=0.200mm，按合理的接法测量时，毫安表和电压表的示数如图丙所示，则毫安表的读数为______ mA，电压表的读数______ V，可求得该卷漆包线的长度 L=______ m．

①在“利用打点计时器测速度”的实验中，运用______法，可以利用打点计时器打出的纸带测算出某点的瞬时速度：在“探究互成角度的两个力的合成”的实验中，分别用一个力F或两个互成角度的F₁、F₂，把一个一端固定的橡皮筋拉伸到同一位置，则F就是F₁和F₂的合力，实验原理采用的是______法．在“探究平抛运动的规律”的实验中，如图1所示，用小锤打击弹性金属片，金属片把A球沿水平方向抛出，同时B球松开，自由下落，A、B两球同时开始运动，观察到两球同时落地．运用______法，可以判定平抛运动在竖直方向上的分运动是自由落体运动．
②图象法是物理实验中一种重要的研究方法．在研究加速度与外力（质量m一定）的关系、验证机械能守恒定律、探究弹
力大小与弹簧伸长量之间的关系三个实验中，某同学正确作出了三个实验的相关图象，如图2中A、B、C所示．根据坐标轴代表的物理量判断，A实验的图象“斜率”表示______；B实验图象的“斜率”表示______；C实验图象的“斜率”表示______．
（2）某一小型电风扇额定电压为4.0V，额定功率为2.4W．某实验小组想通过实验描绘出小电风扇的伏安特性曲线．实验中除导线和开关外，还有以下器材可供选择：
A．电源E（电动势为4.5V）
B．电压表V（量程为0～5V，内阻约为4kΩ）
C．电流表A₁（量程为0～0.6A，内阻约为0.2Ω）
D．电流表A₂（量程3A，内阻约0.05Ω）；
E．滑动变阻器R₁（最大阻值10Ω，额定电流1A）
F．滑动变阻器R₂（最大阻值2kΩ，额定电流100mA）
①为了便于调节，减小读数误差和系统误差，实验中所用电流表应选用______，滑动变阻器应选用______．（填所选仪器前的字母序号）．
②请你为该小组设计实验电路，并把电路图画在虚线内（小电风扇的电路符号如图3所示）．
③操作过程中发现，小电风扇通电后受阻力作用，电压表读数小于0.5V时电风扇没启动．该小组测绘出的小电风扇的伏安特性曲线如图4所示，由此可以判定，小电风扇的电阻为______，正常工作时的发热功率为______，机械功率为______．

试题分类