题目内容
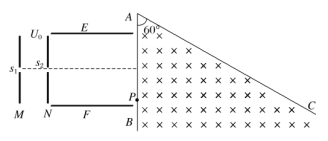
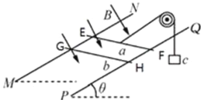
【题目】如图所示，在倾角θ=30°的斜面上固定两根足够长的光滑平行金属导轨PQ、MN，相距为L，导轨处于磁感应强度为B的匀强磁场中，磁场方向垂直导轨平面向下。两根质量均为m的金属棒a、b分别垂直放置在导轨上EF、GH位置，其中a 棒用平行于导轨的细线跨过光滑定滑轮与重物c 连接。已知EF上方导轨的电阻与到EF的距离x有关，EF下方的导轨没有电阻。现在由静止释放a、b、c，a、c一起以加速度
做匀加速运动，b棒刚好仍静止在导轨上。a棒在运动过程中始终与导轨垂直，a、b棒电阻不计，与导轨电接触良好。
（1）求重物c的质量；
（2）求EF上方每根导轨的电阻与到EF的距离x之间的关系；
（3）某时刻t，与a棒连接的细线突然被拉断，求细线被拉断的瞬间a 棒的加速度大小；
（4）在第（3）问中，假设细线被拉断的瞬间，a、b棒的重力突然消失。求从释放a、b、c 到a、b棒的速度稳定过程中，a棒克服安培力做的功。
【答案】（1）3m（2）r=
（3）g（4）
mg2t2
【解析】
（1）设重物c 的质量为M．对a棒，由牛顿定律得
T﹣mgsinθ﹣BIL=ma ①
对重物c，由牛顿定律得
Mg﹣T=Ma ②
对b棒，由平衡条件得
BIL=mgsinθ ③
由①②③式解得
M=3m；
（2）对a、b棒构成的回路，由闭合电路欧姆定律得
BLat=2rI ④
对a棒由运动学公式得
⑤
由 ③、④、⑤式解得
（3）细线被拉断的瞬间，a 棒受安培力不变，对a 棒由牛顿定律得
ma′=mgsinθ+BIL ⑥
由③、⑥式解得：
a′=g；
（4）细线被拉断后，在安培力作用下，b棒向上做加速运动，a棒向上做减速运动，a棒和b棒上的电流大小总是相等，安培力大小总是相等，加速度大小总是相等，所以相等时间内速度变化量大小相等，直至a、b棒构成回路的磁通量不变化，即a、b棒构成回路的面积不变化，即二者以共同速度做匀速直线运动为止．共同速度满足
v同=vb=△v
且
v同=va=at﹣△v ⑦
解得
⑧
从释放a、b、c 到细线刚被拉断的过程中，a 棒克服安培力做的功：
⑨
从细线刚被拉断到a、b 棒的速度稳定（即二者以共同速度匀速直线运动）的过程中，对a 棒由动能定理可得a 棒克服安培力做的功
⑩
由 ③、⑧、⑨、⑩式解得
