题目内容
13. 如图所示,在大气中有一竖直放置的固定圆筒,它由a、b和c三个粗细不同的部分连接而成,各部分的横截面积分别为2S、$\frac{1}{2}$S和S.己知大气压强为P0,温度为T0.两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞在如图所示位置平衡.活塞与圆筒壁之间的摩擦可忽略.己知活塞A质量为2m,活塞B质量为m,重力加速度为g.
如图所示,在大气中有一竖直放置的固定圆筒,它由a、b和c三个粗细不同的部分连接而成,各部分的横截面积分别为2S、$\frac{1}{2}$S和S.己知大气压强为P0,温度为T0.两活塞A和B用一根长为4l的不可伸长的轻线相连,把温度为T0的空气密封在两活塞之间,此时两活塞在如图所示位置平衡.活塞与圆筒壁之间的摩擦可忽略.己知活塞A质量为2m,活塞B质量为m,重力加速度为g.(1)求此时密封气体的压强;
(2)现对被密封的气体加热,使其温度缓慢上升,判断活塞将如何移动;(不要求写出具体过程)
(3)若加热后气体温度缓慢上升到T,此时两活塞之间气体的压强为多少.
分析 (1)分别对两个活塞受力分析列方程,求得压强
(2)加热后活塞将一起向上移动
(3)加热前体积V1=2SL+SL+SL=4SL;加热时,活塞向上移动,体积增大,压强P1保持不变,持续加热,活塞向上移动距离等于L,此时:V2=4SL+SL=5SL,应用理想气体状态方程求解压强.
解答 解:(1)设线的张力为T,对活塞A:2P0S-2P1S+T+2mg=0
对活塞B:P1S-P0S-T+mg=0
联立得:P1=${P}_{0}+\frac{3mg}{S}$
T=4mg
(2)加热后活塞将一起向上移动
(3)加热前体积V1=2SL+SL+SL=4SL
加热时,活塞向上移动,体积增大,压强P1保持不变,持续加热,活塞向上移动距离等于L,此时:V2=4SL+SL=5SL此时温度为T2
则:$\frac{{V}_{2}}{{T}_{2}}=\frac{{V}_{1}}{{T}_{0}}$
解得:${T}_{2}=\frac{5}{4}{T}_{0}$
当T<T2时,P2=P1=${P}_{0}+\frac{3mg}{S}$
当T>T2时,活塞已经无法移动,体积不变,当温度为T时,压强为P,
则:$\frac{P}{T}=\frac{{P}_{1}}{{T}_{2}}$
解得:P=$\frac{4T}{5{T}_{0}}$P1=$\frac{4T}{5{T}_{0}}({P}_{0}+\frac{3mg}{S})$
答:(1)此时密封气体的压强${P}_{0}+\frac{3mg}{S}$;
(2)加热后活塞将一起向上移动
(3)若加热后气体温度缓慢上升到T,此时两活塞之间气体的压强为$\frac{4T}{5{T}_{0}}({P}_{0}+\frac{3mg}{S})$
点评 本题的难点在于对活塞的受力分析及体积大小变化,结合理想气体状态方程求解,难点较大.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
| A. | 大量处在n=4能级的氢原子向低能级跃迁过程中可能发出红外线 | |
| B. | 大量处在n=3能级的氢原子向n=2能级跃迁时,发出的光是紫外线 | |
| C. | 大量处在n=4能级的氢原子向低能级跃迁时,最容易表现出衍射现象的是由n=4向n=3能级跃迁辐射出的光子 | |
| D. | 用能量为10.3eV的电子轰击,可以使基态的氢原子受激发 |
| A. | 每个气体分子都运动得更快 | |
| B. | 气体内能不变 | |
| C. | 单位时间,单位面积容器壁受到的冲量不变 | |
| D. | 单位时间,撞击到单位面积容器壁的分子数增加 |
 带有活塞的气缸内封闭一定质量的理想气体.气体开始处于状态a,然后经过程I到达状态b或经过程Ⅱ到达状态c,如图所示.已知$\frac{P_a}{P_c}<\frac{V_c}{V_a}$,则有( )
带有活塞的气缸内封闭一定质量的理想气体.气体开始处于状态a,然后经过程I到达状态b或经过程Ⅱ到达状态c,如图所示.已知$\frac{P_a}{P_c}<\frac{V_c}{V_a}$,则有( )| A. | 过程Ⅱ可能为等温膨胀过程 | |
| B. | 过程Ⅱ可能为绝热膨胀过程 | |
| C. | 过程Ⅰ与过程Ⅱ气体都从外界吸热,但过程Ⅰ吸收的热量更多 | |
| D. | 过程Ⅰ与过程Ⅱ气体都从外界吸热,但过程Ⅱ吸收的热量更多 |
 如图所示为演示气体定律的趣味仪器--哈勃瓶,它是一个瓶颈很短的平底大烧瓶,在瓶内塞有一气球,气球的吹气口反扣在瓶口上.在一次实验中,瓶内在气球和瓶壁之间封闭一定质量的气体,在对气球缓慢吹气的过程中,当瓶内气体体积减小△V时,压强增大20%.若使瓶内气体体积减小3△V,则其压强增大( )
如图所示为演示气体定律的趣味仪器--哈勃瓶,它是一个瓶颈很短的平底大烧瓶,在瓶内塞有一气球,气球的吹气口反扣在瓶口上.在一次实验中,瓶内在气球和瓶壁之间封闭一定质量的气体,在对气球缓慢吹气的过程中,当瓶内气体体积减小△V时,压强增大20%.若使瓶内气体体积减小3△V,则其压强增大( )| A. | 150% | B. | 100% | C. | 60% | D. | 50% |
 家用台式计算机上的硬磁盘的磁道如图所示,O点为磁道的圆心,A、B两点位于不同的磁道上,硬盘绕O点匀速转动时,有关A、B两点的说法正确的是( )
家用台式计算机上的硬磁盘的磁道如图所示,O点为磁道的圆心,A、B两点位于不同的磁道上,硬盘绕O点匀速转动时,有关A、B两点的说法正确的是( )| A. | A点角速度小于B点角速度 | B. | A点线速度小于B点线速度 | ||
| C. | A点向心加速度大于B点向心加速度 | D. | A、B两点向心加速度方向相同 |
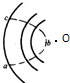 如图所示,一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面,不计重力,可以判断( )
如图所示,一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面,不计重力,可以判断( )| A. | 此粒子可能受到静电吸引力的作用 | |
| B. | b点的电势一定大于在a点的电势 | |
| C. | 粒子在a点和c点的速度一定相同 | |
| D. | 粒子在b点的电势能一定大于在a点的电势能 |
 如图所示,竖直放置的半圆形绝缘轨道的半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中,一质量为m带电荷量为+q的物块(可视为质点)从水平面上的A点以初速度功水平向左运动-沿半圆形轨道恰好能通过能最高点c已知电场强度大小为E(E<$\frac{mg}{q}$,g为重力加速度)
如图所示,竖直放置的半圆形绝缘轨道的半径为R,下端与光滑绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场中,一质量为m带电荷量为+q的物块(可视为质点)从水平面上的A点以初速度功水平向左运动-沿半圆形轨道恰好能通过能最高点c已知电场强度大小为E(E<$\frac{mg}{q}$,g为重力加速度) 在“压强P一热力学温度T”的坐标系中,一定质量的某种理想气体先后经历以下两种变化过程:先从状态A到状态B,该过程中气体从外界吸收热量为6J;再从状态B到状态C,该过程中外界对该气体做功为9J.求:
在“压强P一热力学温度T”的坐标系中,一定质量的某种理想气体先后经历以下两种变化过程:先从状态A到状态B,该过程中气体从外界吸收热量为6J;再从状态B到状态C,该过程中外界对该气体做功为9J.求: