Question

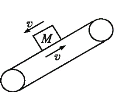
【题目】如图所示，光滑水平面上放着长L＝2 m，质量为M＝4 kg的薄木板，一个质量为m＝1 kg的小物体放在木板的最右端，m和M之间的动摩擦因数μ＝0.2，开始均静止．现对木板施加一水平向右的恒定拉力F，g取10 m/s2．求：

（1）为使小物体不从木板上掉下，F不能超过多少；

（2）如果拉力F＝11N，小物体能获得的最大速度；

（3）如果拉力F＝11 N作用了t＝1s后即撤去，小物体能获得的最大速度．

Answer 1

【答案】(1) 10N (2) 8m/s (3) 2.2m/s

【解析】

(1)物体随木板运动的最大加速度为a，对小物体由牛顿第二定律：μmg=ma
所以可得小物体最大加速度为：

a=μg=0.2×10 =2m/s2

对整体分析，由牛顿第二定律得：

Fm=（M+m）a=（4+1）×2=10N

(2) 因施加的拉力F＞10N，故物体相对木板相对滑动，木板对地运动的加速度为a1，
对木板由牛顿第二定律：F-μmg=Ma1
物块在木板上相对运动的时间为t，有：

解得：

t=4s

物块脱离木板时的速度最大为：

vm=at=8m/s

(3) 因施加的拉力F＞10N，故物体相对木板相对滑动，木板对地运动的加速度为a1，
对木板由牛顿第二定律：F-μmg=Ma1
解得：

由上可知t＝1s时，物体并未脱离木块，此时

物体的速度为：

物体的位移为：

木板的速度为：

木板的位移为：

撤去外力后，物体的加速度为：

a=μg=0.2×10 =2m/s2

木板的加速度为：a2=0.5m/s2

木板和物块共速时间为：v2-a2t2=v1+at2

代入数据解得：

t2=0.1s

此过程中物体的位移为：

木板的位移为：

物块相对木板滑动的距离为：

所以物块将会与木板相对静止，且此时物块速度最大，即