题目内容
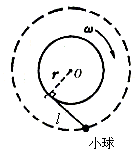
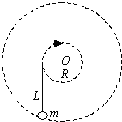如图所示，用手握着一绳端在水平桌面上做半径为R，角速度为ω 的匀速圆周运动，圆心为O，绳长为L，质量不计，绳的另一端系着一个质量为m的小球，恰好也沿着一个以O为圆心的大圆在桌面上做匀速圆周运动，且使绳始终与半径为R的圆相切，小球和桌面之间有摩擦，试求：（1）小球作匀速圆周运动的线速度的大小，
（2）小球在运动过程中所受到的摩擦阻力大小，
（3）手拉动小球做功的功率P．
分析：（1）根据线速度与角速度关系公式v=ωr列式求解；
（2）小球竖直方向受重力和支持力，平面内受拉力T和摩擦力f，拉力T和摩擦力f的合力提供向心力，根据牛顿第二定律并运用合成法求解；
（3）小球做匀速圆周运动，根据动能定理列式求解手拉动小球做功的功率P．
（2）小球竖直方向受重力和支持力，平面内受拉力T和摩擦力f，拉力T和摩擦力f的合力提供向心力，根据牛顿第二定律并运用合成法求解；
（3）小球做匀速圆周运动，根据动能定理列式求解手拉动小球做功的功率P．
解答：解：（1）小球做匀速圆周运动，角速度为ω，转动半径为
，故线速度为：v=ωr=ω
；
（2）小球竖直方向受重力和支持力，平面内受拉力T和摩擦力f，拉力T和摩擦力f的合力提供向心力，如图所示：
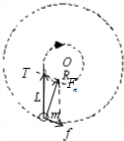
根据几何关系，有：
=
①
根据牛顿第二定律，有：
Fn=mω2
②
联立①②解得：f=
；
（3）小球做匀速圆周运动，根据动能定理，拉力的功率等于克服摩擦力做功的功率，故：
P=fv=
?ω
=
；
答：（1）小球作匀速圆周运动的线速度的大小为ω
；
（2）小球在运动过程中所受到的摩擦阻力大小为
；
（3）手拉动小球做功的功率P为
．
| L2+R2 |
| L2+R2 |
（2）小球竖直方向受重力和支持力，平面内受拉力T和摩擦力f，拉力T和摩擦力f的合力提供向心力，如图所示：
根据几何关系，有：
| Fn |
| L |
| f |
| R |
根据牛顿第二定律，有：
Fn=mω2
| L2+R2 |
联立①②解得：f=
mω2R
| ||
| L |
（3）小球做匀速圆周运动，根据动能定理，拉力的功率等于克服摩擦力做功的功率，故：
P=fv=
mω2R
| ||
| L |
| L2+R2 |
| mω3R(L2+R2) |
| L |
答：（1）小球作匀速圆周运动的线速度的大小为ω
| L2+R2 |
（2）小球在运动过程中所受到的摩擦阻力大小为
mω2R
| ||
| L |
（3）手拉动小球做功的功率P为
| mω3R(L2+R2) |
| L |
点评：本题关键找到向心力来源，然后根据牛顿第二定律和动能定理列式分析，不难．
练习册系列答案
名校课堂系列答案
相关题目
（1）下面是某同学做“验证机械能守恒”实验中的部分实验步骤，请完成填空部分：
的匀速圆周运动，绳的方向恰好能够始终与该圆相切，并使得小球也在同一平面内做半径更大的匀速圆周运动。已知此时人的手给绳的拉力大小恒为T，请利用以上条件推导并表达：