题目内容
 (2011?湖南模拟)如图所示,两根足够长的光滑平行金属导轨相距为l=0.5m,导轨平面与水平面间的夹角θ=30°,整个导轨平面处于匀强磁场中,磁场的磁感应强度大小B=0.4T,方向垂直导轨平面,在导轨上垂直导轨放置两金属棒ab和cd,长度均为0 5m,cd棒的质量m=0.2kg、电阻R=0.2Ω,不计ab棒和金属导轨的电阻,两棒与金属导轨接触良好且可沿导轨自由滑动.现ab棒在外力作用下,始终以恒定速度v=1.5m/s沿着导轨向上滑动,cd棒则由静止释放,g取10m/s2.求:
(2011?湖南模拟)如图所示,两根足够长的光滑平行金属导轨相距为l=0.5m,导轨平面与水平面间的夹角θ=30°,整个导轨平面处于匀强磁场中,磁场的磁感应强度大小B=0.4T,方向垂直导轨平面,在导轨上垂直导轨放置两金属棒ab和cd,长度均为0 5m,cd棒的质量m=0.2kg、电阻R=0.2Ω,不计ab棒和金属导轨的电阻,两棒与金属导轨接触良好且可沿导轨自由滑动.现ab棒在外力作用下,始终以恒定速度v=1.5m/s沿着导轨向上滑动,cd棒则由静止释放,g取10m/s2.求:(1)刚释放cd棒时cd棒所受合力的大小和方向;
(2)闭合回路中的最大电流和金属棒cd的最终速度.
分析:(1)金属棒ab以恒定速度v=1.5m/s运动,切割磁感线产生感应电动势,由公式E=Blv求出感应电动势,由欧姆定律求出感应电流,求出cd棒所受安培力有大小和方向,再求解cd棒所受合力的大小和方向.
(2)释放cd棒后,cd棒沿导轨平面向下做加速运动,回路abdc中产生的感应电动势逐渐增大,感应电流逐渐增大,cd所受的安培力增大,合力减小,加速度减小,当合力减小到零时,cd棒做匀速直线运动,速度达到最大,回路中的电流也达到最大.以cd为研究对象,由平衡条件求出最大电流.此时回路中感应电动势为ab与cd两棒所产生的感应电动势之和,由欧姆定律和公式电动势结合求解最大速度.
(2)释放cd棒后,cd棒沿导轨平面向下做加速运动,回路abdc中产生的感应电动势逐渐增大,感应电流逐渐增大,cd所受的安培力增大,合力减小,加速度减小,当合力减小到零时,cd棒做匀速直线运动,速度达到最大,回路中的电流也达到最大.以cd为研究对象,由平衡条件求出最大电流.此时回路中感应电动势为ab与cd两棒所产生的感应电动势之和,由欧姆定律和公式电动势结合求解最大速度.
解答:解:(1)db棒产生的感应电动势E=Blv=0.3V
刚释放时cd棒时,由欧姆定律得
I=
=1.5A
cd所受安培力大小为F安=BIl=0.3N,由左手定则判断可知,安培力方向沿导轨向上.
则cd棒所受合力的大小F=mgsin30°-F安=0.7N,方向沿导轨向下.
(2)释放cd棒后,cd棒沿导轨向下先做加速运动,后做匀速运动,则匀速运动时速度最大,设为vm,回路中感应电流最大,设为Im.以cd棒为研究对象,由平衡条件得:
mgsin30°=BIml
代入解得 Im=5A
回路中的感应电动势为Em=Bl(v+vm)
又由欧姆定律得 Em=ImR
则联立解得 vm=3.5m/s
答:(1)刚释放cd棒所受合力的大小为0.7N,方向沿导轨向下.
(2)闭合回路中的最大电流为5A,金属棒cd的最终速度为3.5m/s.
刚释放时cd棒时,由欧姆定律得
I=
| E |
| R |
cd所受安培力大小为F安=BIl=0.3N,由左手定则判断可知,安培力方向沿导轨向上.
则cd棒所受合力的大小F=mgsin30°-F安=0.7N,方向沿导轨向下.
(2)释放cd棒后,cd棒沿导轨向下先做加速运动,后做匀速运动,则匀速运动时速度最大,设为vm,回路中感应电流最大,设为Im.以cd棒为研究对象,由平衡条件得:
mgsin30°=BIml
代入解得 Im=5A
回路中的感应电动势为Em=Bl(v+vm)
又由欧姆定律得 Em=ImR
则联立解得 vm=3.5m/s
答:(1)刚释放cd棒所受合力的大小为0.7N,方向沿导轨向下.
(2)闭合回路中的最大电流为5A,金属棒cd的最终速度为3.5m/s.
点评:本题是电磁感应中的力学问题,综合运用电磁学知识和力平衡知识.对于第(2)问是两棒切割磁感线类型,要注意回路中感应电动势等于两棒产生的感应电动势之和.

练习册系列答案
相关题目
 (2011?湖南模拟)如图所示,一条易断的均匀细绳两端固定在天花板上的A、B两点,今在绳上某点O处固定悬挂砝码,使AO=2BO,则( )
(2011?湖南模拟)如图所示,一条易断的均匀细绳两端固定在天花板上的A、B两点,今在绳上某点O处固定悬挂砝码,使AO=2BO,则( )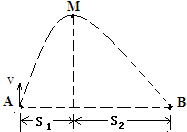 (2011?湖南模拟)在大风的情况下,一小球自A点竖直上抛,其运动轨迹如图所示,(小球的运动可看作竖直方向的竖直上抛运动和水平方向的初速度为零的匀加速直线运动的合运动),小球运动轨迹上A、B两点在同一水平直线上,M点为轨迹的最高点.若风力的大小恒定,方向水平向右,小球在A点抛出时的动能为4J,在M点时它的动能为2J,落回到B点时动能记为EKB,小球上升时间记为t1,下落时间记为t2,不计其它阻力,则( )
(2011?湖南模拟)在大风的情况下,一小球自A点竖直上抛,其运动轨迹如图所示,(小球的运动可看作竖直方向的竖直上抛运动和水平方向的初速度为零的匀加速直线运动的合运动),小球运动轨迹上A、B两点在同一水平直线上,M点为轨迹的最高点.若风力的大小恒定,方向水平向右,小球在A点抛出时的动能为4J,在M点时它的动能为2J,落回到B点时动能记为EKB,小球上升时间记为t1,下落时间记为t2,不计其它阻力,则( ) (2011?湖南模拟)用油膜法估测分子的大小实验中,求油膜面积时,用边长为1cm的正方形方格坐标纸得到油膜轮廓线如图所示,则该油膜的面积为
(2011?湖南模拟)用油膜法估测分子的大小实验中,求油膜面积时,用边长为1cm的正方形方格坐标纸得到油膜轮廓线如图所示,则该油膜的面积为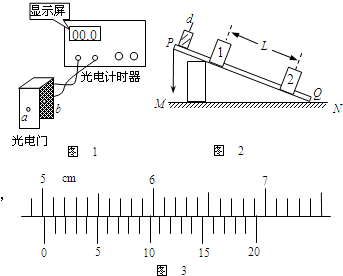 (2011?湖南模拟)像打点计时器一样,光电计时器也是一种研究物体运动情况的常用计时仪器,其结构如图1所示,a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.现利用图2所示装置测量滑块经过斜面上相隔lm左右的两个光电门时的速度,图中MN是水平桌面,Q是木板与桌面的接触点,1和2是固定在木板上适当位置的两个光电门,与之连接的两个光电计时器没有画出.让滑块从木板的顶端滑下,光电门l、2各自连接的计时器显示的挡光时间分别为5.0×10-2s和2.0×10-2s.用游标卡尺测量小滑块的宽度d,示数如图3所示.
(2011?湖南模拟)像打点计时器一样,光电计时器也是一种研究物体运动情况的常用计时仪器,其结构如图1所示,a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.现利用图2所示装置测量滑块经过斜面上相隔lm左右的两个光电门时的速度,图中MN是水平桌面,Q是木板与桌面的接触点,1和2是固定在木板上适当位置的两个光电门,与之连接的两个光电计时器没有画出.让滑块从木板的顶端滑下,光电门l、2各自连接的计时器显示的挡光时间分别为5.0×10-2s和2.0×10-2s.用游标卡尺测量小滑块的宽度d,示数如图3所示. (2011?湖南模拟)(1)现有a、b、c三束单色光,其波长关系为λa>λb>λt,用b光束照射某种金属时,恰能发生光电效应.若分别用a、b、c光束照射该金属,则可以断定
(2011?湖南模拟)(1)现有a、b、c三束单色光,其波长关系为λa>λb>λt,用b光束照射某种金属时,恰能发生光电效应.若分别用a、b、c光束照射该金属,则可以断定