题目内容
6.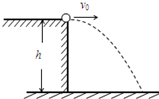 现有一个小铁球在h=20m高台边缘处被水平抛出,如图所示,初速度v0=10m/s,不计空气阻力.(g取10m/s2)求:
现有一个小铁球在h=20m高台边缘处被水平抛出,如图所示,初速度v0=10m/s,不计空气阻力.(g取10m/s2)求:(1)从抛出到落地,小铁球运动的时间是多少?
(2)小铁球水平飞出多远?
(3)小铁球落地时的速度v是多少?
分析 (1)根据平抛运动的规律,小球在竖直方向做自由落体运动,知道高度可以求出时间;
(2)小球在水平方向做匀速运动,知道时间和初速度就可以求出小球运动的水平距离;
(3)先求出竖直分速度,根据速度的合成求出小球落地时的速度大小.
解答 解:(1)小铁球在竖直方向做自由落体运动,根据:$h=\frac{1}{2}g{t}^{2}$
得 $t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×20}{10}}=2$s
(2)水平方向做匀速直线运动,所以:x=v0t=10×2=20m
(3)竖直方向的速度:vy=gt=10×2=20m,
水平方向速度为:v0=10m/s
所以$v=\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{1{0}^{2}+2{0}^{2}}=10\sqrt{5}$
设落地时其速度方向与水平方向的夹角为θ,则
$tanθ=\frac{{v}_{y}}{{v}_{0}}=\frac{20}{10}=2$,
故θ=arctan2
答:(1)小球在空中运动的时间为2s;
(2)小球运动的水平距离为20m;
(3)小球落地时的速度大小为10$\sqrt{5}$m/s.落地时其速度方向与水平方向的夹角为arctan2.
点评 解决本题的关键是掌握平抛运动的性质,知道平抛运动如何分解,明确其运动时间是高度决定的.

练习册系列答案
相关题目
16.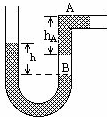 如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
 如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )
如图所示,U形管两臂竖直固定,右管中一段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,A有部分水银在水平管中,设U形管内粗细均匀,两端均开口与大气相通.现保持温度不变,向左管缓慢注入少量水银,则重新平衡后( )| A. | 图中h减小 | B. | 空气柱B的长度不变 | ||
| C. | 空气柱B的压强增大 | D. | 图中h不变 |
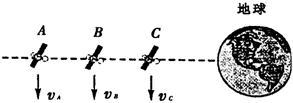
14.如图所示,在同一轨道平面上的几个人造地球卫星A、B、C绕地球做匀速圆周运动,某一时刻恰好在同一直线上,下列说法中正确的是( )

| A. | 根据v=$\sqrt{gr}$可知,运行速度满足vA>vB>vC | |
| B. | 向心加速度满足aA<aB<aC | |
| C. | 运转角速度满足ωA>ωB>ωC | |
| D. | 运动一周后,A最先回到图示位置 |
11.下列关于运动和力的叙述中,正确的是( )
| A. | 做曲线运动的物体,其加速度一定是变化的 | |
| B. | 物体所受合力方向与运动方向相同,该物体一定做直线运动 | |
| C. | 匀速圆周运动是加速度不变的运动 | |
| D. | 物体运动的速率在增加,所受合力方向一定与运动方向相同 |
18.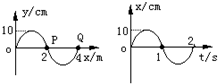 如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )
如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )
 如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )
如图所示,为一简谐横波在t=1s时的波形图和该波上一质点P的振动图象,根据图象可知,下列说法正确的是( )| A. | Q点速度向y轴负方向 | B. | P点振幅为5cm | ||
| C. | 波沿x轴正方向传播,v=10m/s | D. | 波沿x轴负方向传播,v=2m/s |
1. 在雾霾严重地区,有同学想通过静电除尘的方法净化空气,设计原理图如图所示.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.第一种除尘方式是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;第二种除尘方式是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,则在这两种方式中正确的是( )
在雾霾严重地区,有同学想通过静电除尘的方法净化空气,设计原理图如图所示.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.第一种除尘方式是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;第二种除尘方式是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,则在这两种方式中正确的是( )
 在雾霾严重地区,有同学想通过静电除尘的方法净化空气,设计原理图如图所示.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.第一种除尘方式是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;第二种除尘方式是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,则在这两种方式中正确的是( )
在雾霾严重地区,有同学想通过静电除尘的方法净化空气,设计原理图如图所示.她用玻璃圆桶密闭含灰尘的空气,圆桶的高和直径相等.第一种除尘方式是:在圆桶顶面和底面间加上电压U,沿圆桶的轴线方向形成一个匀强电场,尘粒的运动方向如图甲所示;第二种除尘方式是:在圆桶轴线处放一直导线,在导线与桶壁间加上的电压也等于U,形成沿半径方向的辐向电场,尘粒的运动方向如图乙所示.已知空气阻力与尘粒运动的速度成正比,即F阻=kv(k为一定值),假设每个尘粒的质量和带电荷量均相同,则在这两种方式中正确的是( )| A. | 尘粒最终一定都做匀速运动 | B. | 尘粒受到的电场力大小相等 | ||
| C. | 电场对单个尘粒做功的最大值相等 | D. | 乙容器中的尘粒运动为类平抛运动 |
 某同学在做《研究平抛物体的运动》实验得到图示运动轨迹,a、b、c三点的位置坐标已经在图上已经标出
某同学在做《研究平抛物体的运动》实验得到图示运动轨迹,a、b、c三点的位置坐标已经在图上已经标出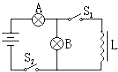 如图所示,A、B是两盏完全相同的白炽灯,L是电阻不计的电感线圈,如果断开开关S1,接通S2,A、B两灯都能同样发光.最初S1是接通的,S2是断开的.那么,可能出现的情况是( )
如图所示,A、B是两盏完全相同的白炽灯,L是电阻不计的电感线圈,如果断开开关S1,接通S2,A、B两灯都能同样发光.最初S1是接通的,S2是断开的.那么,可能出现的情况是( )