题目内容
在水平地面上，有一小球A从某点以初速度v0=6m/s向右做匀加速直线运动．同时，在A球的正上方高h=20m处，另一小球B以速度vB=8m/s向右水平抛出，B球落地时刚好砸在A球上．若不计空气阻力，g=10m/s2，求：
（1）两小球相碰时，A球所前进的位移s；
（2）两小球相碰时，A球的速度vt及加速度a．
（1）两小球相碰时，A球所前进的位移s；
（2）两小球相碰时，A球的速度vt及加速度a．
分析：球A是匀加速直线运动，而球B是平抛运动，由于同时运动又相碰，则在相同的时间内，球A的位移与球B的水平位移相等．从而利用竖直位移求出运动的时间，最终可求出球A的位移、速度及加速度．
解答：解：
（1）根据题意可知：球A做匀加速直线运动，而球B做平抛运动，两球相碰表明，A、B两球在水平方向上的位移相等：A球水平运动时间恰好等于B球从高20m处自由落下时间，即
由 h=
gt2得：t=
=2s
所以 sB水平=vBt=16m
则A球前进的位移也为16m．
（2）∵
t=sB水平
∴vA=12m/s
由 vA=vAO+at
得：a=2m/s2
答：（1）A球前进的位移为16m；（2）A球的速度为12m/s；加速度为2m/s2．
（1）根据题意可知：球A做匀加速直线运动，而球B做平抛运动，两球相碰表明，A、B两球在水平方向上的位移相等：A球水平运动时间恰好等于B球从高20m处自由落下时间，即
由 h=
| 1 |
| 2 |
|
所以 sB水平=vBt=16m
则A球前进的位移也为16m．
（2）∵
| vAO+vA |
| 2 |
∴vA=12m/s
由 vA=vAO+at
得：a=2m/s2
答：（1）A球前进的位移为16m；（2）A球的速度为12m/s；加速度为2m/s2．
点评：球A虽是匀加速直线运动，但只知道一初速度是无法求其它量，通过相碰则借助于球B的可得知球A的运动的位移，从而算出球A的速度与加速度．
练习册系列答案
阅读快车系列答案
相关题目
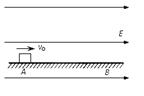
在粗糙的水平地面上，有一小滑块，质量为m=1kg，带正电荷，带电量为q=10-3C，整个空间充满着水平向右的匀强电场，电场强度为E=3×103 N/C，滑块与地面间的动摩擦因数μ=0.4．在地面A处，滑块开始以水平向右的初速度v0=2m/s向右滑动，最后在B处停下，重力加速度取g=10m/s2，求：（1）滑块在水平地面上滑动的距离xAB；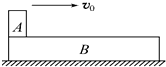
如图所示，一足够长的木板B静止在水平地面上，有一小滑块A以v0=2m/s的水平初速度冲上该木板．已知木板质量是小滑块质量的2倍，木板与小滑块间的动摩擦因数为μ1=0.5，木板与水平地面间的动摩擦因数为μ2=0.1，求小滑块相对木板滑行的位移是
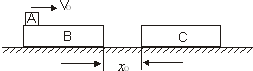如图所示，木板B、C长度均为6米，静止在水平地面上，有一小滑块A以VO=6m/s的水平初速度冲上A木板左端，已知mB=mC=2mO，mA=mO．木板与小滑块间的动摩擦因数为u1=0.5，木板B、C与水平地面间的动摩擦因数为 u2=0.1．B与C之间距离xO=0.5米．求：
