题目内容
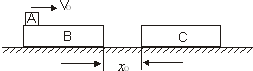 如图所示,木板B、C长度均为6米,静止在水平地面上,有一小滑块A以VO=6m/s的水平初速度冲上A木板左端,已知mB=mC=2mO,mA=mO.木板与小滑块间的动摩擦因数为u1=0.5,木板B、C与水平地面间的动摩擦因数为 u2=0.1.B与C之间距离xO=0.5米.求:
如图所示,木板B、C长度均为6米,静止在水平地面上,有一小滑块A以VO=6m/s的水平初速度冲上A木板左端,已知mB=mC=2mO,mA=mO.木板与小滑块间的动摩擦因数为u1=0.5,木板B、C与水平地面间的动摩擦因数为 u2=0.1.B与C之间距离xO=0.5米.求:(1)B与C碰击前小滑块相对木板滑行的距离是多少?
(2)B与C碰后粘在一起,A在B上滑动的总距离是多少?
(3)B最终相对地面运动的距离是多少?
分析:(1)B与C碰撞前,对A和B分别受力分析,根据牛顿第二定律分别求出A和B的加速度,分析B产生0.5m位移时A所产生的位移,则其两者之差为滑块A在B上滑行的距离;
(2)B与C碰撞瞬间满足动量守恒,据此求出BC碰撞后的共同速度,再分别分析滑块A和BC共同体的运动,当两者速度相等时的两者位移差即可求出A在B上滑行的总距离;
(3)当ABC三者具有共同速度时,在地面摩擦力作用下一起做匀减速直线运动求出匀减速直线运动的位移.滑块B分别在匀加速运动、匀速运动和匀减速运动三段运动位移之和即为B最终相对地面运动的距离.
(2)B与C碰撞瞬间满足动量守恒,据此求出BC碰撞后的共同速度,再分别分析滑块A和BC共同体的运动,当两者速度相等时的两者位移差即可求出A在B上滑行的总距离;
(3)当ABC三者具有共同速度时,在地面摩擦力作用下一起做匀减速直线运动求出匀减速直线运动的位移.滑块B分别在匀加速运动、匀速运动和匀减速运动三段运动位移之和即为B最终相对地面运动的距离.
解答:解:(1)对A进行受力分析有:
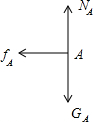
有:F合=fA=μNA=μmAg=μm0g
根据牛顿第二定律有滑块A产生的加速度aA=
=μ1g=5m/s2
对B进行受力分析有:
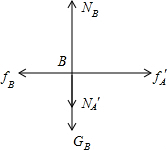
B受到5个力作用,重力GB=2m0g,A对B的压力
=m0g,地面的支持力NB,A对B的摩擦力
=fA=μ1m0g,和地面对B的摩擦力fB=μ2NB
所以B所受合力F合B=fA′-fB=μ1m0g-μ2NB
B产生的加速度aB=
=
=
m/s2=1m/s2
由此分析知,A滑块做匀减速直线运动,B滑块做匀加速直线运动,当两者速度相等时有:
vA=vA0-aAt
vB=aBt
即:vA0-aAt=vBt代入数据可解得:
t=1s
此时滑块A的位移xA=vA0t-
aAt2=6×1-
×5×12m=3.5m
此时滑块B的位移xB=
aBt2=
×1×12m=0.5m
因为B滑块滑动0.5m后刚好与C滑块相碰,故在相碰前,A在B上滑行的距离:
△xA=xA-xB=3m
(2)B与C碰撞后根据动量守恒可得碰撞后BC共同体的速度v,由(1)分析知碰撞前刚好是AB速度相等时,即此时vA=vB=aBt=1m/s,碰撞过程遵循动量守恒有:
mBvB+mCvC=(mB+mC)v
则其共同速度v=
=
m/s=0.5m/s
此时对A分析,
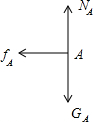
A产生的加速度aA=5m/s2
对BC组合本进行受力分析有:
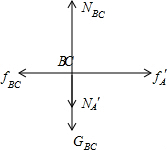
BC在水平平方向所受合力F合=fA′-fBC=μ1m0g-μ2(2m0+2m0+m0)g=0,即此时BC组合体在水平面上将作匀速直线运动.
所以当A的速度由vA=1m/s减速为和组合体速度一致时有
A产生的位移:xA1=
=
m=0.075m
此时BC组合体产生的位移xBC=vt=v×
=0.5×
m=0.05m
则此时A在B上滑动的位移△xA1=xA1-xBC=0.025m
所以A在B上滑行的总距离为S=△xA+△xA1=3.025m
(3)由(2)分析知,当A滑块的速度减为和BC速度相同时则ABC将在地面摩擦力的作用下做匀匀减速直线运动,此时以整体为研究对象受力分析有:
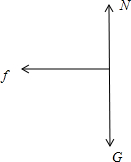
可知,整体所受合力F合=f=μ2G=μ2Mg
根据牛顿第二定律有,整体产生的加速度a=
=μ2g=1m/s2
整体的初速度为v=0.5m/s,所以整体做匀减速直线运动的位移
x3=
=
m=0.125m
所以整个过程中B相对地面运动位移
xB总=xB+xBC+x3=0.5+0.05+0.125m=0.675m
答:(1)B与C碰击前小滑块相对木板滑行的距离是3m
(2)B与C碰后粘在一起,A在B上滑动的总距离是3.025m
(3)B最终相对地面运动的距离是0.675m
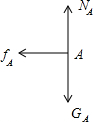
有:F合=fA=μNA=μmAg=μm0g
根据牛顿第二定律有滑块A产生的加速度aA=
| F合 |
| m0 |
对B进行受力分析有:

B受到5个力作用,重力GB=2m0g,A对B的压力
| N | ′ A |
| f | ′ A |
所以B所受合力F合B=fA′-fB=μ1m0g-μ2NB
B产生的加速度aB=
| F合B |
| mB |
| μ1m0g-μ2(m0+2m0)g |
| 2m0 |
| 0.5×10-0.1×3×10 |
| 2 |
由此分析知,A滑块做匀减速直线运动,B滑块做匀加速直线运动,当两者速度相等时有:
vA=vA0-aAt
vB=aBt
即:vA0-aAt=vBt代入数据可解得:
t=1s
此时滑块A的位移xA=vA0t-
| 1 |
| 2 |
| 1 |
| 2 |
此时滑块B的位移xB=
| 1 |
| 2 |
| 1 |
| 2 |
因为B滑块滑动0.5m后刚好与C滑块相碰,故在相碰前,A在B上滑行的距离:
△xA=xA-xB=3m
(2)B与C碰撞后根据动量守恒可得碰撞后BC共同体的速度v,由(1)分析知碰撞前刚好是AB速度相等时,即此时vA=vB=aBt=1m/s,碰撞过程遵循动量守恒有:
mBvB+mCvC=(mB+mC)v
则其共同速度v=
| mBvB+mCvC |
| mB+mC |
| 2m0×1 |
| 2m0+2m0 |
此时对A分析,
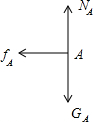
A产生的加速度aA=5m/s2
对BC组合本进行受力分析有:

BC在水平平方向所受合力F合=fA′-fBC=μ1m0g-μ2(2m0+2m0+m0)g=0,即此时BC组合体在水平面上将作匀速直线运动.
所以当A的速度由vA=1m/s减速为和组合体速度一致时有
A产生的位移:xA1=
v2-
| ||
| -2aA |
| 0.52-12 |
| -2×5 |
此时BC组合体产生的位移xBC=vt=v×
| v-vA |
| -aA |
| 0.5-1 |
| -5 |
则此时A在B上滑动的位移△xA1=xA1-xBC=0.025m
所以A在B上滑行的总距离为S=△xA+△xA1=3.025m
(3)由(2)分析知,当A滑块的速度减为和BC速度相同时则ABC将在地面摩擦力的作用下做匀匀减速直线运动,此时以整体为研究对象受力分析有:

可知,整体所受合力F合=f=μ2G=μ2Mg
根据牛顿第二定律有,整体产生的加速度a=
| F合 |
| M |
整体的初速度为v=0.5m/s,所以整体做匀减速直线运动的位移
x3=
| v2 |
| 2a |
| 0.52 |
| 2×1 |
所以整个过程中B相对地面运动位移
xB总=xB+xBC+x3=0.5+0.05+0.125m=0.675m
答:(1)B与C碰击前小滑块相对木板滑行的距离是3m
(2)B与C碰后粘在一起,A在B上滑动的总距离是3.025m
(3)B最终相对地面运动的距离是0.675m
点评:本题主要考查连接体问题,主要学会运用整体法和隔离法对物体进行受力分析和运动分析是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,木板B放在水平地面上,木块A放在B上,一根弹性细绳左端固定在A的右侧,绳的右端固定在墙上,细绳保持水平,现用力F水平向左拉B,并维持它以速度V运动,此情况下细绳上的拉力大小为T,现有下列分析,其中正确的是( )
如图所示,木板B放在水平地面上,木块A放在B上,一根弹性细绳左端固定在A的右侧,绳的右端固定在墙上,细绳保持水平,现用力F水平向左拉B,并维持它以速度V运动,此情况下细绳上的拉力大小为T,现有下列分析,其中正确的是( )| A、木板B受到的滑动摩擦力大小等于T | B、木块A受到的滑动摩擦力大小等于(F-T) | C、地面受到的滑动摩擦力大小等于F | D、木块A与木板B间的滑动摩擦力大小等于T |
 如图所示,木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a到最低点b的过程中( )
如图所示,木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a到最低点b的过程中( ) (2011?西湖区模拟)如图所示,木板B托着木块A在竖直平面内做匀速圆周运动.从水平位置a到最高点b的过程中( )
(2011?西湖区模拟)如图所示,木板B托着木块A在竖直平面内做匀速圆周运动.从水平位置a到最高点b的过程中( )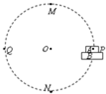 如图所示,木板B上放置一物体A,用手托着木板使其与A一起在竖直平面内做顺时针匀速圆周运动,A、B均可视为质点,运动过程中A与木板保持相对静止,且木板始终水平.图中P、Q点为运动轨迹上与圆心O同高度的两点,M、N分别为轨迹的最高点和最低点,则( )
如图所示,木板B上放置一物体A,用手托着木板使其与A一起在竖直平面内做顺时针匀速圆周运动,A、B均可视为质点,运动过程中A与木板保持相对静止,且木板始终水平.图中P、Q点为运动轨迹上与圆心O同高度的两点,M、N分别为轨迹的最高点和最低点,则( )