题目内容
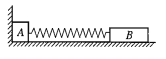
【题目】如图，足够长的水平直道与倾斜光滑轨道BC平滑连接，B为光滑轨道的最低点。小球从直道上的A点以v0＝
m/s的初速度向右运动，与静止在B点的小球b发生弹性正碰，碰撞后小球b上升的最大高度h＝0.2m。已知A、B两点的距离x＝0.5m，小球与水平直道的摩擦阻力f为重力的0.1倍，空气阻力忽略不计，重力加速度g＝10m/s2。求：
（1）两球相碰前的瞬间小球的速度大小。
（2）两球相碰后的瞬间小球b的速度大小。
（3）小球和小球b的质量之比。
【答案】(1) 
(2) 
(3) 
【解析】
（1）设小球a与小球b碰撞前瞬间的速度为
，由动能定理：
①
其中
②，带入数据得：
③
（2）设a、b两球碰撞后b球的速度为
，小球b碰后沿光滑轨道上升的过程中机械能守恒。由机械能守恒定律：
④，解得：
⑤
（3）a、b两球发生弹性碰撞。设碰撞后a球的速度为
，由动量和机械能守恒定律有：
⑥，
⑦
由⑥⑦得：
⑧，由③⑤⑧得：
练习册系列答案
相关题目
