题目内容
11.在十字路口,汽车以2m/s2的加速度从停车线启动做匀加速运动,恰好有一辆自行车以10m/s的速度匀速驶过停车线与汽车同方向行驶,求:(1)什么时候(几秒后)它们相距最远?最远距离是多少?
(2)在什么地方汽车追上自行车?追到时汽车的速度是多大?
分析 (1)在汽车速度没有达到自行车速度之前,两者的距离是越来越大,当两者速度相等时,距离将保持不变,当汽车速度大于自行车速度时,两者距离逐渐减小.抓住相距最远的临界条件(两者速度相等)利用匀变速直线运动的规律可求相距最远的时间及最远距离.
(2)汽车做初速度为0的匀加速直线运动,自行车做匀速直线运动,汽车追上自行车时,两者相对于停车线的位移相等,利用位移相等可求相遇所需的时间t,利用v=v0+at可得追上时汽车的速度v.
解答 解:(1)由题意分析知,当两车速度相等时相距最远,设所用时间为t,汽车做初速度为0的匀加速直线运动,所以有:
v汽=at=v自
已知a=2m/s2,v自=10m/s,
可得:t=5s
最远距离为:
x=x自-x汽=v自t-$\frac{1}{2}$at2=25m.
(2)汽车追上自行车时,它们相对于停车线的位移相等,设汽车追上自行车所用时间为t′,此时有:
x自=x汽
即:v自t′=$\frac{1}{2}$at/2
代入a=2m/s2
v自=10m/s
可得:t′=10s
此时距停车线距离为:x=v自t′=100m
此时汽车速度为:v汽=a t′=20m/s
答:(1)汽车运动5s时它们相距最远,最远距离为25m;
(2)汽车在距停车线100m处追上自行车,追上自行车时汽车的速度为20m/s.
点评 追击问题的临界条件,相距最远时两者速度相等,这是条件,追上时是指两物体在同一时刻处于同一位置,若起点相同,则两物体的位移应该相等.

练习册系列答案
相关题目
1. 两个质点甲和乙,同时由同一地点向同一方向做直线运动,它们的v-t图象如图所示,则下列说法中正确的是( )
两个质点甲和乙,同时由同一地点向同一方向做直线运动,它们的v-t图象如图所示,则下列说法中正确的是( )
 两个质点甲和乙,同时由同一地点向同一方向做直线运动,它们的v-t图象如图所示,则下列说法中正确的是( )
两个质点甲和乙,同时由同一地点向同一方向做直线运动,它们的v-t图象如图所示,则下列说法中正确的是( )| A. | 质点乙静止,质点甲的初速度为零 | B. | 第1s末质点甲、乙速度方向不一样 | ||
| C. | 第2s末质点甲、乙速度相同 | D. | 第2s末质点甲、乙相遇 |
2.下列说法错误的是( )
| A. | 磁极间的相互作用是通过磁场发生的 | |
| B. | 磁场和电场一样是客观存在的物质 | |
| C. | 磁场就像磁感线一样是条形的 | |
| D. | 磁感线可以表示出磁场的强弱 |
20.如图所示,人站在自动扶梯的水平踏板上,随扶梯斜向上匀速运动,以下说法正确的是( )


| A. | 人受到重力和支持力的作用 | |
| B. | 人受到重力、支持力和摩擦力的作用 | |
| C. | 人的重力和踏板对人的支持力是一对平衡力 | |
| D. | 人对踏板的压力就是人的重力 |
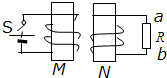 如图所示,通电螺线管M右侧放一个连接外电阻R的螺线管N,当S断开时,R中的感应电流的方向是由b到a.
如图所示,通电螺线管M右侧放一个连接外电阻R的螺线管N,当S断开时,R中的感应电流的方向是由b到a. 如图所示,在光滑水平面上,一质量为1kg的小球A以v0=10m/s的速度向右运动,与静止的质量为5kg的B球发生正碰,若碰后A球以$\frac{1}{2}$v0的速度反弹,则:
如图所示,在光滑水平面上,一质量为1kg的小球A以v0=10m/s的速度向右运动,与静止的质量为5kg的B球发生正碰,若碰后A球以$\frac{1}{2}$v0的速度反弹,则: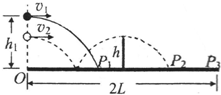 抛体运动在各类体育运动项目中很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,如图所示,且不考虑乒乓球的旋转和空气阻力.(设重力加速度为g)
抛体运动在各类体育运动项目中很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,如图所示,且不考虑乒乓球的旋转和空气阻力.(设重力加速度为g)

