题目内容
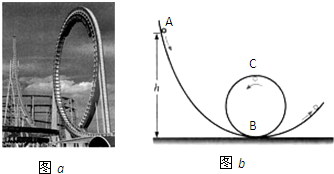
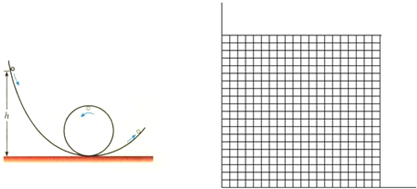
（B）游乐场的过山车可以底朝天在圆轨道上运行，游客却不会掉下来．我们把这种情况抽象为如图的模型：弧形轨道的下端与竖直圆轨道相接，使小球从弧形轨道上端滚下，小球进入圆轨道下端后沿圆轨道运动，小球由静止放开时的位置比轨道最低点高出h．实验发现，只要h大于一定值，小球就可以顺利通过圆轨道的最高点．如果已知圆轨道的半径为R=0.2m，取g=10m/s2，不考虑摩擦等阻力．（1）h至少要等于多大，小球才能恰好通过最高点？
（2）若小球通过最高点时，对轨道的压力不大于重力，求h的范围？
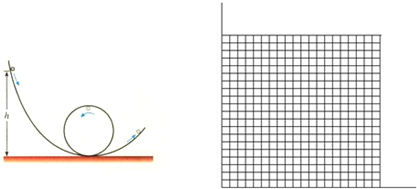
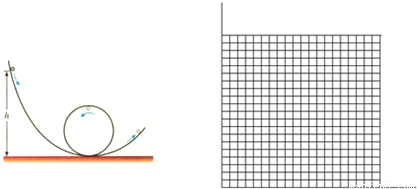
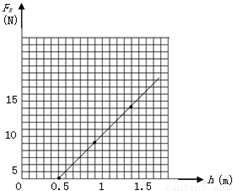
（3）改变h的数值，用压力传感器测出小球到达轨道最高点时对轨道的压力大小FN，试通过计算在纸上作出FN-h图象（已知小球质量0.1kg）
【答案】分析：（1）根据过山车能通过圆形轨道最高点得出在最高点的速度值，根据运动过程机械能守恒求解．
（2）压力恰好等于重力时，重力和弹力的合力提供向心力，根据牛顿第二定律列式求解．
（3）根据机械能守恒定律列式；再根据重力和弹力的合力提供向心力列式；然后联立求解得到FN与h的关系并画出图象．
解答：解：（1）由机械能守恒定律：mg（h-2R）=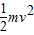
小球在最高点：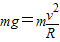
所以：h=2.5R=0.5m
（2）小球在最高点：mg+FN=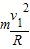
根据题意FN≤mg
所以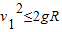
根据机械能守恒定律，有：mg（h′-2R）=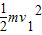
解得h′≤3R=0.6m
所以H的范围从0.5-0.6m
（3）根据机械能守恒定律，有：mg（h-2R）=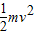
在最高点，合力提供向心力，根据牛顿第二定律，有：FN+mg=m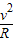
两式联立得到：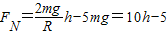
，图象如图所示；
答：（1）h至少要等于0.5m，小球才能恰好通过最高点；
（2）若小球通过最高点时，对轨道的压力不大于重力，则h的范围为：0.5m≤h≤0.6m；
（3）如图所示．
点评：本题关键是明确小球的运动规律，知道圆轨道最高点重力和支持力的合力提供向心力，同时要结合机械能守恒定律列式求解，较难．
（2）压力恰好等于重力时，重力和弹力的合力提供向心力，根据牛顿第二定律列式求解．
（3）根据机械能守恒定律列式；再根据重力和弹力的合力提供向心力列式；然后联立求解得到FN与h的关系并画出图象．
解答：解：（1）由机械能守恒定律：mg（h-2R）=
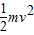
小球在最高点：
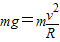
所以：h=2.5R=0.5m
（2）小球在最高点：mg+FN=
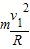
根据题意FN≤mg
所以
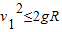
根据机械能守恒定律，有：mg（h′-2R）=
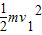
解得h′≤3R=0.6m
所以H的范围从0.5-0.6m
（3）根据机械能守恒定律，有：mg（h-2R）=
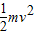
在最高点，合力提供向心力，根据牛顿第二定律，有：FN+mg=m
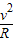
两式联立得到：
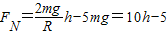，图象如图所示；答：（1）h至少要等于0.5m，小球才能恰好通过最高点；
（2）若小球通过最高点时，对轨道的压力不大于重力，则h的范围为：0.5m≤h≤0.6m；
（3）如图所示．
点评：本题关键是明确小球的运动规律，知道圆轨道最高点重力和支持力的合力提供向心力，同时要结合机械能守恒定律列式求解，较难．
练习册系列答案
相关题目
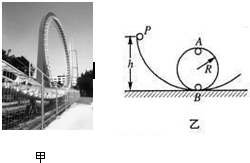游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来（如图甲）．我们把这种情况抽象为图乙的模型：弧形轨道的下端与竖直圆轨道相接，使小球从弧形轨道上端无初速滚下，小球进入圆轨道下端后沿圆轨道运动（不计摩擦和空气阻力），其中A、B分别为圆轨道的最低点和最高点．若质量为m的小球从曲面轨道上的P点由静止开始下滑，并且可以顺利通过半径为R的圆轨道的最高点A．已知P点与B点的高度差h=3R，求：
