题目内容
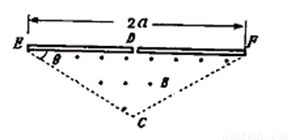
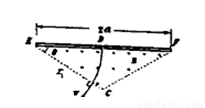
如图所示，在一底边长为2a，θ=30°的等腰三角形区域内（D在底边中点），有垂直纸面向外的匀强磁场．现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从D点垂直于EF进入磁场，不计重力和与空气阻力的影响．
（1）若粒子恰好垂直于EC边射出磁场，求磁场的磁感应强度B为多少？
（2）改变磁感应强度的大小，粒子进入磁场偏转后能打到ED板，求粒子从进入磁场到第一次打到ED板的最长时间是多少？
（3）改变磁感应强度的大小，可以再延长粒子在磁场中的运动时间，求粒子在磁场中运动的极限时间．（不计粒子与ED板碰撞的作用时间．设粒子与ED板碰撞前后，电量保持不变并以相同的速率反弹）
(1)依题意，粒子经电场加速射入磁场时的速度为v
由
得
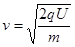………………① （１分）
粒子在磁场中做匀速圆周运动其圆心在E点，如图所示，半径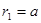
…………②
由洛仑兹力提供向心力：
………③ （１分）
由①②③式得：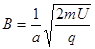
（2分）
(2) 粒子速率恒定，从进入磁场到第一次打到ED板的圆周轨迹到EC边相切时,路程最长，运动时间最长．如图，设 圆周半径为r2
由图中几何关系：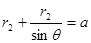 
得： 
……………④ （2分）
最长时间 
………⑤ （2分）
由①④⑤式得：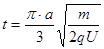
（2分）
(3) 设粒子运动圆周半径为r，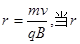
越小，后一次打到ED板的点越靠近E端点,在磁场中圆周运动累积路程越大，时间越长．当r为无穷小，经过n个半圆运动,最后一次打到E点．
有： 
………………⑥
（２分）
圆周运动周期：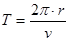 
…………⑦ （1分）
最长的极限时间： 
…………⑧ （３分）
由⑥⑦⑧式得： 
（２分）
【解析】略
（2011?山西模拟）如图所示，在一底边长为2a，θ=30°的等腰三角形区域内（D在底边中点），有垂直纸面向外的匀强磁场．现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从D点垂直于EF进入磁场，不计重力和与空气阻力的影响．
（2013?山西模拟）如图所示，在一底边长为2L、髙为L的等腰直角三角形区域分布着如图所示的匀强 磁场，左侧磁场方向垂直纸面向外．右侧磁场方向垂直纸面向里，磁感应强度大小均为 B．一边长为L、总电阻为R的正方形导线框必abcd，从图示位置开始沿x轴E方向以速 率v匀速运动并穿过磁场区域．取沿a→b→c→d→a方向．的感应电流 为正，则图乙中表示线框中电流i随 bc边的位置坐标x变化的图象正确 的是（ ）
如图所示，在一底边长为2L，θ=45°的等腰三角形区域内（O为底边中点）有垂直纸面向外的匀强磁场．现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从O点垂直于AB进入磁场，不计重力与空气阻力的影响．
如图所示，在一底边长为2L，θ=45°的等腰三角形区域内（O为B边中点）有垂直纸面向外的匀强磁场．现有一质量为m，电量为q的带负电粒子从静止由A板开始经过电势差为U的电场加速后，从O点垂直于B进入磁场，不计重力与空气阻力的影响．
，
°的等腰三角形区域内（D在底边中点，）有垂直纸面向外的匀强磁场，现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从D点垂直于EF进入磁场，不计重力和空气阻力的影响。