题目内容
8.某同学用打点计时器测量做匀加速直线运动的物体的加速度,电源频率f=50Hz.在选出的纸带上,确定起始计数点O后,每5个实际打点定为1个计数点,如图中A、B、C、D所示.因保存不当,纸带被污染,仅读出A、B、D等3个计数点到O点的距离:xA=16.6mm,xB=126.5mm,xD=624.5mm.可由以上信息推知:
(1)相邻两计数点的时间间隔为0.1s,
(2)打C点时物体的速度大小为2.5m/s;(取2位有效数字)
(3)物体的加速度大小为$\frac{({x}_{D}-{x}_{B})-2({x}_{B}-{x}_{A}){f}^{2}}{75}$.(用xA、xB、xD和f等题中给出字母表示)
分析 纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.
解答 解:(1)每5个实际打点定为1个计数点,则相邻两计数点的时间间隔为T=0.1s.
(2)根据间的平均速度等于点的速度得vc=$\frac{{x}_{BD}}{{t}_{BD}}=\frac{0.6245-0.1265}{0.2}$=2.5m/s.
(3)匀加速运动的位移特征是相邻的相等时间间隔内的位移以aT2均匀增大,即△x=aT2,所以有:
xBC=xAB+aT2,xCD=xBC+aT2=xAB+2aT2,xBD=2xAB+3aT2,
所以a=$\frac{({x}_{D}-{x}_{B})-2({x}_{B}-{x}_{A})}{3{T}^{2}}$=$\frac{({x}_{D}-{x}_{B})-2({x}_{B}-{x}_{A}){f}^{2}}{75}$
故答案为:(1)0.1;(2)2.5;(3)$\frac{({x}_{D}-{x}_{B})-2({x}_{B}-{x}_{A}){f}^{2}}{75}$
点评 要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用,注意单位的换算和有效数字的保留.

练习册系列答案
相关题目
16.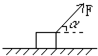 如图所示,位于水平地面上质量为m的木块,在大小为F方向与水平方向成α角的拉力的作用下沿地面作匀加速运动,若木块与地面间动摩擦因数为μ,则木块的加速度大小为( )
如图所示,位于水平地面上质量为m的木块,在大小为F方向与水平方向成α角的拉力的作用下沿地面作匀加速运动,若木块与地面间动摩擦因数为μ,则木块的加速度大小为( )
 如图所示,位于水平地面上质量为m的木块,在大小为F方向与水平方向成α角的拉力的作用下沿地面作匀加速运动,若木块与地面间动摩擦因数为μ,则木块的加速度大小为( )
如图所示,位于水平地面上质量为m的木块,在大小为F方向与水平方向成α角的拉力的作用下沿地面作匀加速运动,若木块与地面间动摩擦因数为μ,则木块的加速度大小为( )| A. | $\frac{F}{m}$ | B. | $\frac{Fcosα}{m}$ | ||
| C. | $\frac{(Fcosα-μmg)}{m}$ | D. | $\frac{[Fcosα-μ(mg-Fsinα)]}{m}$ |
3. 目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )
目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )
 目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )
目前,我市每个社区均已配备了公共体育健身器材.图示器材为一秋千,用两根等长轻绳将一座椅悬挂在竖直支架上等高的两点.由于长期使用,导致两根支架向内发生了稍小倾斜,如图中虚线所示,但两悬挂点仍等高.座椅静止时单根轻绳对座椅拉力的大小,与倾斜前相比( )| A. | 变小 | B. | 变大 | C. | 不变 | D. | 无法确定 |
17.示波器中重要的组成部分之一是示波管,如图所示为示波管的示意图,以屏幕的中心为坐标原点,建立如图所示的直角坐标系xoy,当在XX′这对电极上加上恒定的电压UXX′=2V,同时在YY′电极上加上恒定的电压UYY′=-1V时,荧光屏上光点的坐标为(4,-1),则当在XX′这对电极上加上恒定的电压UXX′=3V,同时在YY′电极上加上恒定的电压UYY′=4V时,荧光屏上光点的坐标为( )
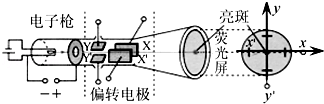

| A. | (6,2) | B. | (2,-2) | C. | (6,-2) | D. | (6,4) |
18.关于滑动摩擦力,下列说法正确的是( )
| A. | 物体在支持面上的滑动速度越大,滑动摩擦力也一定越大 | |
| B. | 滑动摩擦力的方向一定与物体运动方向相反 | |
| C. | 滑动摩擦力的方向一定与物体相对支持面的滑动方向相反 | |
| D. | 滑动摩擦力一定发生在运动的物体间 |
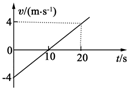 一质点做直线运动,t=0时,位于坐标原点,如图为质点做直线运动的速度-时间图象.由图可知:
一质点做直线运动,t=0时,位于坐标原点,如图为质点做直线运动的速度-时间图象.由图可知: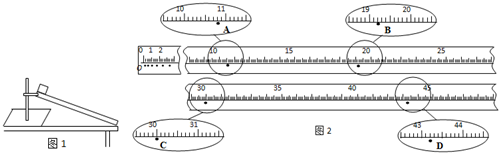
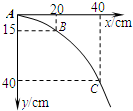 某同学在做研究平抛物体运动规律的实验时得到了如图所示的小球的运动轨迹,A、B、C三点的位置在运动轨迹上已标出.其中A点的坐标为(0,0),g=10m/s2,则
某同学在做研究平抛物体运动规律的实验时得到了如图所示的小球的运动轨迹,A、B、C三点的位置在运动轨迹上已标出.其中A点的坐标为(0,0),g=10m/s2,则