��Ŀ����
14��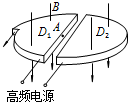 �������������������ٴ������ӵ�װ�ã���ͼΪ������������ʾ��ͼ��D1��D2�������пյ����ư�Բ�ν�����У�������D�κ����м俪��һ�����죬����D�κн��ڸ�Ƶ������Դ�ϣ���D1������A��������Դ�������Ĵ���������������֮�䱻�糡���ٺ����D2���У�����D�κд�������洹ֱ����ǿ�ų��У����������ڴų�����������������Բ���˶����������Բ�ܺ��ٴε������м�����죬���ƽ�����Դ��ѹ�����ڣ���֤�������Ӿ�������ʱ�ٴα����٣���ˣ���������Բ���˶��Ĺ�����һ��һ�εؾ������죬һ��һ�εر����٣��ٶ�Խ��Խ���˶��뾶ҲԽ��Խ�����D�κеı�Ե�������߷���������ٶȱ���������֪�������ӵĵ����Ϊq������Ϊm������ʱ������ѹ��С��ΪU���ų��ĴŸ�Ӧǿ��ΪB��D�κеİ뾶ΪR������֮��ľ���Ϊd���������Դ�����Ĵ������ӵij��ٶ�Ϊ�㣬���������ܵ�����������
�������������������ٴ������ӵ�װ�ã���ͼΪ������������ʾ��ͼ��D1��D2�������пյ����ư�Բ�ν�����У�������D�κ����м俪��һ�����죬����D�κн��ڸ�Ƶ������Դ�ϣ���D1������A��������Դ�������Ĵ���������������֮�䱻�糡���ٺ����D2���У�����D�κд�������洹ֱ����ǿ�ų��У����������ڴų�����������������Բ���˶����������Բ�ܺ��ٴε������м�����죬���ƽ�����Դ��ѹ�����ڣ���֤�������Ӿ�������ʱ�ٴα����٣���ˣ���������Բ���˶��Ĺ�����һ��һ�εؾ������죬һ��һ�εر����٣��ٶ�Խ��Խ���˶��뾶ҲԽ��Խ�����D�κеı�Ե�������߷���������ٶȱ���������֪�������ӵĵ����Ϊq������Ϊm������ʱ������ѹ��С��ΪU���ų��ĴŸ�Ӧǿ��ΪB��D�κеİ뾶ΪR������֮��ľ���Ϊd���������Դ�����Ĵ������ӵij��ٶ�Ϊ�㣬���������ܵ�������������1�����������ܱ����ٵ������Ek��
��2������������D2���е�n����Բ�İ뾶��
��3���������������ӻ������������ʱ�γɵĵ�Ч����ΪI����ӻ�������������Ĵ������ӵ�ƽ������$\overline P$��
���� ��1������qvB=m$\frac{{v}^{2}}{R}$֪����R���ʱ���ٶ�����������ٶȣ�����EK=$\frac{1}{2}$mv2������ӵ�����ܣ�
��2�����ӱ�����һ������õ�����ΪqU�������n�μ��ٺ�Ķ���EKn=$\frac{1}{2}$mvn2=$\frac{{q}^{2}{B}^{2}{R}_{n}^{2}}{2m}$=��2n-1��qU�������������n����Բ�İ뾶��
��3�����ݵ����Ķ���ʽI=$\frac{Q}{t}$��Q=Nq�Լ�P=$\frac{N•\frac{1}{2}m{v}^{2}}{t}$��������⣮
��� �⣺��1��������D�κ�����Բ���˶�������뾶�ﵽ���ʱ����������������ܣ�
���ʱ���ٶ�Ϊv���У�qvB=m$\frac{{v}^{2}}{R}$
�ɵ�v=$\frac{qBR}{m}$
���ӵ������Ek=$\frac{1}{2}$mv2=$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$
��2�����ӱ�����һ������õ�����ΪqU��������D2���б���n�μ��ٺ�Ķ���Ϊ
EKn=$\frac{1}{2}$mvn2=$\frac{{q}^{2}{B}^{2}{R}_{n}^{2}}{2m}$=��2n-1��qU��
��˵�n����Բ�İ뾶Rn=$\frac{1}{Bq}\sqrt{2��2n-1��qmU}$��
��3��������������Ϊm�������Ϊq�����������뿪������ʱ�ٶȴ�СΪv����ţ�ٵڶ�����֪��qvB=m$\frac{{v}^{2}}{R}$����
���������˶��Ļ�������Ϊ��T=$\frac{2��R}{v}$=$\frac{2��m}{qB}$����
�ɻ�������������ԭ����֪�������Դ��Ƶ����������ӻ���Ƶ����ͬ��������T��Ƶ��f�Ĺ�ϵ�ɵã�f=$\frac{1}{T}$����
����tʱ�����뿪�������Ĵ���������ΪN��������������ӻ������������ʱ��ƽ������P=$\frac{N•\frac{1}{2}m{v}^{2}}{t}$����
���ʱ�����������ĵ�Ч����Ϊ��I=$\frac{Nq}{t}$����
��������ʽ��$\overline{P}$=$\frac{��BI{R}^{2}}{T}$=$\frac{{B}^{2}{R}^{2}Iq}{2m}$��
�𣺣�1�����������ܱ����ٵ������$\frac{{q}^{2}{B}^{2}{R}^{2}}{2m}$��
��2������������D2���е�n����Բ�İ뾶$\frac{1}{Bq}\sqrt{2��2n-1��qmU}$��
��3���������������ӻ������������ʱ�γɵĵ�Ч����ΪI����ӻ�������������Ĵ������ӵ�ƽ������$\frac{{B}^{2}{R}^{2}Iq}{2m}$��
���� �������Ĺؼ�֪���������������ôų�ƫת�͵糡����ʵ�ּ������ӣ������ڴų����˶������ںͽ������������ȣ�ע���3���⣬������ȷ������ģ���ǽ���Ĺؼ���

 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д� ��ͼ��2008��4��16�ձ������˻���ڰͻ�˹̹��˹��������ʱ����ͳ��������ͬ����潻���˶�Ա��ʱ�̣����й��ڻ����Ħ������˵������ȷ���ǣ�������
��ͼ��2008��4��16�ձ������˻���ڰͻ�˹̹��˹��������ʱ����ͳ��������ͬ����潻���˶�Ա��ʱ�̣����й��ڻ����Ħ������˵������ȷ���ǣ�������| A�� | �ܵ����Ǿ�Ħ���� | B�� | �ܵ����ǻ���Ħ���� | ||
| C�� | Ħ�������ڻ������ | D�� | Ħ�������ڻ������ |
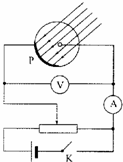 ��ͼ�������K�Ͽ�ʱ���ù�������Ϊ2.1eV��һ������������P�����ֵ�����������Ϊ�㣮 ���ϵ�������ڻ��߱����������ֵ���ѹ������С��0.40Vʱ�������������Բ�Ϊ�㣻����ѹ���������ڻ����0.40Vʱ������������Ϊ�㣻�ɴ˿�֪�������ϵ��ݳ���Ϊ��������
��ͼ�������K�Ͽ�ʱ���ù�������Ϊ2.1eV��һ������������P�����ֵ�����������Ϊ�㣮 ���ϵ�������ڻ��߱����������ֵ���ѹ������С��0.40Vʱ�������������Բ�Ϊ�㣻����ѹ���������ڻ����0.40Vʱ������������Ϊ�㣻�ɴ˿�֪�������ϵ��ݳ���Ϊ��������| A�� | 0.4eV | B�� | 1.7eV | C�� | 2.1eV | D�� | 2.5eV |
 ��ͼ4��ʾ��һ��ֱ��Ϊd��ֽ��ԲͲ�Խ��ٶȦ�������������ת����һ�ӵ���AO������ֽͲ����ֽͲת��������ʱ���ӵ���ֽͲ��������һ������B����֪��AOB=�ȣ����ӵ��ٶ�vΪ��������
��ͼ4��ʾ��һ��ֱ��Ϊd��ֽ��ԲͲ�Խ��ٶȦ�������������ת����һ�ӵ���AO������ֽͲ����ֽͲת��������ʱ���ӵ���ֽͲ��������һ������B����֪��AOB=�ȣ����ӵ��ٶ�vΪ��������| A�� | 2��d | B�� | $\frac{��d}{2��}$ | C�� | $\frac{��d}{��}$ | D�� | $\frac{��d}{����-�ȣ�}$ |
| A�� | ���� | B�� | ���� | C�� | ���� | D�� | ��ȷ�� |
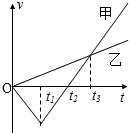 �������ʵ��ͬһ�ص�ͬʱ��ʼ��ͬһֱ�����˶���ȡ��ʼ�˶���ʱ��t=0�����ǵ�v-tͼ����ͼ��ʾ��������
�������ʵ��ͬһ�ص�ͬʱ��ʼ��ͬһֱ�����˶���ȡ��ʼ�˶���ʱ��t=0�����ǵ�v-tͼ����ͼ��ʾ��������| A�� | ����t1ʱ�̸ı��˶����� | B�� | ��t2ʱ�̣����������Զ | ||
| C�� | ��t3ʱ�̣�����λ����ͬ | D�� | ��t3ʱ�̣����������Զ |
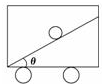 ������ˮƽֱ�����ȼ����˶����ڳ�������һ��װ����ʾ��С����⻬б����Ծ�ֹ��б����ˮƽ��ļн�Ϊ�ȣ�������һ�����жϻļ��ٶȷ���С��
������ˮƽֱ�����ȼ����˶����ڳ�������һ��װ����ʾ��С����⻬б����Ծ�ֹ��б����ˮƽ��ļн�Ϊ�ȣ�������һ�����жϻļ��ٶȷ���С�� ijͬѧ�ڡ���֤����ƽ���ı��ζ���ʵ��ʱ����̽���˵��ɵ�����С�볤�ȹ�ϵ��ʵ��װ����ͼa��ʾ�����ɴ�����ֱ������ͨ��ʵ��õ���ͼ��b����ʾ�ĵ�����СF�뵯�ɳ���x�Ĺ�ϵͼ�ߣ�
ijͬѧ�ڡ���֤����ƽ���ı��ζ���ʵ��ʱ����̽���˵��ɵ�����С�볤�ȹ�ϵ��ʵ��װ����ͼa��ʾ�����ɴ�����ֱ������ͨ��ʵ��õ���ͼ��b����ʾ�ĵ�����СF�뵯�ɳ���x�Ĺ�ϵͼ�ߣ�
 ��ͼ��ʾ��EΪ���費�ܺ��Եĵ�أ�R1��R2��R3��Ϊ��ֵ���裬�����Ϊ����������ʼʱ����S�պϣ�����������ж�����ijʱ�̷��ַ��ر�ʾ����С���������ʾ��������·�п��ܳ��ֵĹ����ǣ�������
��ͼ��ʾ��EΪ���費�ܺ��Եĵ�أ�R1��R2��R3��Ϊ��ֵ���裬�����Ϊ����������ʼʱ����S�պϣ�����������ж�����ijʱ�̷��ַ��ر�ʾ����С���������ʾ��������·�п��ܳ��ֵĹ����ǣ�������