题目内容
11. 出租车是一种方便快捷的交通工具,深受人们的欢迎.平直公路上,一辆质量为m=1.5t的出租车由静止开始做匀加速运动,当速度达到v=2m/s时发现有一乘客招手,于是立即关闭发动机直到停止,其v-t图象如图所示.设出租车所受阻力f大小不变,在加速和减速过程中汽车克服阻力做功分别为W1和W2,出租车牵引力做功为W,则( )
出租车是一种方便快捷的交通工具,深受人们的欢迎.平直公路上,一辆质量为m=1.5t的出租车由静止开始做匀加速运动,当速度达到v=2m/s时发现有一乘客招手,于是立即关闭发动机直到停止,其v-t图象如图所示.设出租车所受阻力f大小不变,在加速和减速过程中汽车克服阻力做功分别为W1和W2,出租车牵引力做功为W,则( )| A. | W=W1+W2 | |
| B. | W1=W2 | |
| C. | 在第1s内出租车所受合外力对出租车做功为W合=3×103J | |
| D. | 出租车的额定功率一定为P=8×103W |
分析 速度时间图象与坐标轴围成的面积表示位移,图象的斜率表示加速度,根据牛顿第二定律求出牵引力,进而求出牵引力做的功,对全过程运用动能定理,抓住动能变化量为零求出全过程中牵引力做功与克服摩擦力做功关系.
解答 解:速度时间图象与坐标轴围成的面积表示位移,由图可知:加速位移和减速位移s:s′=1:3
根据恒力做功公式W=fs可知,${W}_{1}=\frac{1}{3}{W}_{2}$,
对全过程由动能定理可知W-W1-W2=0-0
解得:W=W1+W2,故A正确,B错误;
C、根据图象的斜率表示加速度得:a=$\frac{△v}{△t}=\frac{2}{1}=2m/{s}^{2}$,
则在第1s内出租车所受合外力对出租车做功为W合=mas=$1.5×1{0}^{3}×2×\frac{1}{2}×1×2$=3×103J,故C正确;
D、根据题意无法求出出租车的额定功率,故D错误.
故选:AC.
点评 本题要注意在机车起动中灵活利用功率公式及动能定理公式,同时要注意图象在题目中的应用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
2.如图甲所示,轻杆一端与小球相连,另一端连在光滑固定轴上,可在竖直平面内自由转动,现在最低点给小球以不同的初速度,使其在竖直平面内做圆周运动,到达某一位置开始计时,取水平向右为正方向,当小球的初速度不同时,小球的水平分速度vx随时间t的变化关系如图乙或图丙所示.不计空气阻力.下列说法中正确的是( )
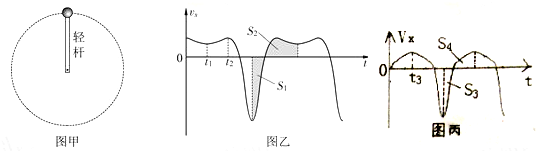

| A. | 在图乙中,t1时刻小球通过最高点,图乙中S1和S2的面积相等 | |
| B. | 在图乙中,t2时刻小球通过最高点,图乙中S1和S2的面积相等 | |
| C. | 在图丙中,t3时刻小球通过最高点,图丙中S3和S4的面积相等 | |
| D. | 图丙中小球的初速度大于图乙中小球的初速度 |
6.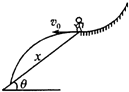 在某次自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞出,在空中划过一段抛物线后,再落到雪坡上,如图所示,若忽略空气阻力,雪坡的倾角为θ,飞出时的速度大小为v0,则下列说法错误的是( )
在某次自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞出,在空中划过一段抛物线后,再落到雪坡上,如图所示,若忽略空气阻力,雪坡的倾角为θ,飞出时的速度大小为v0,则下列说法错误的是( )
 在某次自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞出,在空中划过一段抛物线后,再落到雪坡上,如图所示,若忽略空气阻力,雪坡的倾角为θ,飞出时的速度大小为v0,则下列说法错误的是( )
在某次自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞出,在空中划过一段抛物线后,再落到雪坡上,如图所示,若忽略空气阻力,雪坡的倾角为θ,飞出时的速度大小为v0,则下列说法错误的是( )| A. | 运动员在空中经历的时间是$\frac{2{v}_{0}tanθ}{g}$ | |
| B. | 运动员的落点与起飞点的距离是$\frac{2{{v}^{2}}_{0}sinθ}{gco{s}^{2}θ}$ | |
| C. | 运动员落回斜坡时的速度大小是$\frac{{v}_{0}}{cosθ}$ | |
| D. | 运动员的落点与起飞点间竖直高度是$\frac{2{{v}^{2}}_{0}ta{n}^{2}θ}{g}$ |
16.两个共点力的合力与分力的关系是( )
| A. | 合力大小一定等于两个分力大小之和 | |
| B. | 合力大小一定大于两个分力大小之和 | |
| C. | 合力大小一定大于一个分力的大小,小于另一个分力的大小 | |
| D. | 合力大小可能比两个分力的大小都大,可能都小,也可能比一个分力大,比另一个分力小 |
3.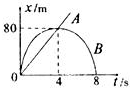 如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )
如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )
 如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )
如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )| A. | A质点做匀加速直线运动 | |
| B. | A、B两质点在8s末相遇 | |
| C. | B质点最初4s做减速运动,后4s做加速运动 | |
| D. | B质点先沿负方向做直线运动,后沿正方向做直线运动 |
1.下列有关力的说法正确的是( )
| A. | 形状规则的物体的重心一定在物体的几何中心上 | |
| B. | 一本书静止放在桌面上,桌面受到的压力产生的直接原因是书本的重力作用 | |
| C. | 正常行驶时汽车后轮对地的摩擦力的方向与汽车的运动方向相反 | |
| D. | 所有弹力的大小都与引起该弹力产生的弹性形变的大小成正比 |
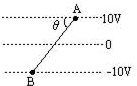 如图是某匀强电场的等势面示意图,A、B相距5cm,θ=53°一带电量为-4×10-6C的微粒沿AB匀速运动,则此电场强度为500N/C,微粒的质量为2×10-4kg.(取g=10m/s2,sin53°=0.8,cos53°=0.6)
如图是某匀强电场的等势面示意图,A、B相距5cm,θ=53°一带电量为-4×10-6C的微粒沿AB匀速运动,则此电场强度为500N/C,微粒的质量为2×10-4kg.(取g=10m/s2,sin53°=0.8,cos53°=0.6) 某同学利用数字化信息系统研究一定质量理想气体的状态变化,实验后计算机屏幕显示如图所示的p-V图象.已知该气体在状态A时的温度为27℃.求:
某同学利用数字化信息系统研究一定质量理想气体的状态变化,实验后计算机屏幕显示如图所示的p-V图象.已知该气体在状态A时的温度为27℃.求: