题目内容
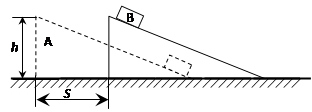
(15分)如图所示,一质量为1 kg的小球套在一根固定的直杆上,直杆与水平面夹角θ为30°。现小球在F="20" N的竖直向上的拉力作用下,从A点静止出发向上运动,已知杆与球间的动摩擦因数μ为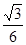 。试求:(1)小球运动的加速度a1;(2)若F作用1.2s后撤去,小球上滑过程中距A点最大距离sm;(3)若从撤去力F开始计时,小球经多长时间将经过距A点上方为2.25 m的B点。
。试求:(1)小球运动的加速度a1;(2)若F作用1.2s后撤去,小球上滑过程中距A点最大距离sm;(3)若从撤去力F开始计时,小球经多长时间将经过距A点上方为2.25 m的B点。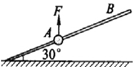
 。试求:(1)小球运动的加速度a1;(2)若F作用1.2s后撤去,小球上滑过程中距A点最大距离sm;(3)若从撤去力F开始计时,小球经多长时间将经过距A点上方为2.25 m的B点。
。试求:(1)小球运动的加速度a1;(2)若F作用1.2s后撤去,小球上滑过程中距A点最大距离sm;(3)若从撤去力F开始计时,小球经多长时间将经过距A点上方为2.25 m的B点。
(1)2.5 m/s2 (2)2.4m (3)0.75s
(1)在力F作用时有:
(F-mg)sin30°-μ(F-mg)cos30°=ma1
a1=2.5 m/s2 (2分)
(2)刚撤去F时,小球的速度v1= a1t1=3m/s 小球的位移s1 = v1/2 t1=1.8m (1分)
撤去力F后,小球上滑时有:
mgsin30°+mmgcos30°=ma2 a2=7.5 m/s2 (1分)
因此小球上滑时间t2="-" v1/ a=0.4s 上滑位移s2= v1t2/2 =0.6m (1分)
则小球上滑的最大距离为sm=2.4m (1分)
(3)在上滑阶段通过B点:
sAB- s1= v1 t3-a2t32 (1分)
通过B点时间 t3=0.2 s ,另t3=0.6s (舍去) (1分)
小球返回时有:mgsin30°-mgcos30°=ma3
a3=2.5 m/s2 (1分)
因此小球由顶端返回B点时有:
sm- sAB =-a3t42 t4 = (1分)
通过B点时间 t2+ t4=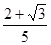 = 0.75s (2分)
= 0.75s (2分)
本题考查对牛顿第二定律的应用,以小球为研究对象,受到重力、拉力、支持力和摩擦力的作用,沿着杆的方向和垂直杆的方向建立直角坐标系,沿着杆的方向的合力提供加速度,垂直杆的方向受力平衡,从而先求得加速度大小,撤去F后小球受到重力和摩擦力作用向上做匀减速直线运动,由运动学公式可求得速度减小到零所需时间,再由位移与时间的关系求得上升的最大位移
(F-mg)sin30°-μ(F-mg)cos30°=ma1
a1=2.5 m/s2 (2分)
(2)刚撤去F时,小球的速度v1= a1t1=3m/s 小球的位移s1 = v1/2 t1=1.8m (1分)
撤去力F后,小球上滑时有:
mgsin30°+mmgcos30°=ma2 a2=7.5 m/s2 (1分)
因此小球上滑时间t2="-" v1/ a=0.4s 上滑位移s2= v1t2/2 =0.6m (1分)
则小球上滑的最大距离为sm=2.4m (1分)
(3)在上滑阶段通过B点:
sAB- s1= v1 t3-a2t32 (1分)
通过B点时间 t3=0.2 s ,另t3=0.6s (舍去) (1分)
小球返回时有:mgsin30°-mgcos30°=ma3
a3=2.5 m/s2 (1分)
因此小球由顶端返回B点时有:
sm- sAB =-a3t42 t4 = (1分)
通过B点时间 t2+ t4=
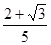 = 0.75s (2分)
= 0.75s (2分)本题考查对牛顿第二定律的应用,以小球为研究对象,受到重力、拉力、支持力和摩擦力的作用,沿着杆的方向和垂直杆的方向建立直角坐标系,沿着杆的方向的合力提供加速度,垂直杆的方向受力平衡,从而先求得加速度大小,撤去F后小球受到重力和摩擦力作用向上做匀减速直线运动,由运动学公式可求得速度减小到零所需时间,再由位移与时间的关系求得上升的最大位移

练习册系列答案
相关题目
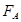 ;
;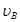 大小。
大小。