题目内容
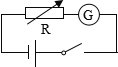
【题目】如图所示.竖直放置的间距为L=1m的两平行光滑导轨,上端连接一个阻值为R=1Ω的电阻,在导轨的MN位置以下有垂直纸面向里的磁场,在MN处的磁感应强度为B0=1T,在MN下方的磁场沿Y轴方向磁感应强度均匀减少,在MN下方1m处的磁感应强度刚好为零.现有一质量为1kg,电阻也是R=1Ω的金属棒,从距离MN为h=0.2m的上方紧贴导轨自由下落,然后进入磁场区域继续下落相同高度h的过程中,能使得电阻R上的电功率保持不变(不计一切摩擦)求(g=10m/s2):

(1)电阻R上的电功率;
(2)从MN位置再下降h时,金属棒的速度v;
(3)从MN位置再下降h所用的时间t.
【答案】(1)1W(2)2.5m/s(3)0.4375s
【解析】(1)由mgh=![]() mv12得v1=2m/s
mv12得v1=2m/s
此时感应电动势为E=B0Lv1=2V
感应电流为![]()
P=I2R=1W
(2)磁感应强度随y的变化关系为:B=B0-ky
当y=1m时,B=0,所以k=1
所以有B=1-y(T)
因为金属棒在磁场中下落h的过程中电阻R上的电功率保持不变,所以感应电动势不变
E=B0Lv1=(1-y)Lv
代入数据得v=2.5m/s
(3)金属棒从MN位置在下降h过程中,由动能定理可知
![]()
带入数据得W克A=0.875J
所以整个过程中产生的焦耳热为:Q=W克A=0.875J
根据焦耳定律可得:Q=2Pt 代入数据可得t=0.4375s

练习册系列答案
相关题目