题目内容
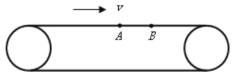
【题目】如图所示，直杆AB与水平面成α角固定，在杆上套一质量为m的小滑块(滑块可视为质点)，杆上各处与滑块之间的动摩擦因数保持不变，杆底端B点处有一弹性挡板，杆与板面垂直，滑块与挡板碰撞后原速率返回。现将滑块拉到A点由静止释放，滑块与挡板第一次碰撞后恰好能上升到AB的中点，设重力加速度为g，下列说法中正确的是
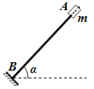
A. 可以求出滑块下滑和上滑过程加速度的大小a1、a2
B. 取过B点的水平面为零势能面，则可以判断滑块从A下滑至B的过程中，重力势能等于动能的位置在AB中点的下方
C. 可以求出滑块在杆上运动的总路程S
D. 可以求出滑块第一次与挡板碰撞时重力做功的瞬时功率P
【答案】AB
【解析】设下滑位移为L，到达底端速度为v，由公式v2=2ax得：
下滑过程：v2=2a2L ①
上滑过程：v2=2a1
=a1L ②
由牛顿第二定律得：
下滑加速度为：
③
上滑加速度为：
④
①②③④联立得：
，
，故A正确；
可以考虑到达AB中点时刻，如果没有摩擦，则机械能守恒，此时动能与重力势能相等；但实际有摩擦，动能偏小，故需要继续下降才可能动能和势能相等，故B正确；将滑块拉到A点由静止释放能够下滑，说明重力的下滑分力大于最大静摩擦力，故最终滑块停在底端；对运动全程，根据动能定理，有：
mgLsinα-μmgcosαS=0-0，
对从释放到第一次反弹到最高点过程，根据动能定理，有：
mgsinα-μmgcosα
L=0-0，
联立解得：
，不知道L，故C错误；由于不知道杆的长度L，故滑块第一次与挡板碰撞时的速度无法求解，也就不能求解此时重力的瞬时功率，故D错误；故选AB.
练习册系列答案
相关题目
