Question

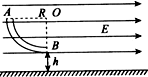（2012?东城区三模）如图所示，水平地面上方分布着水平向右的匀强电场，场强大小为E．一个弯成

1

4

圆周的环状绝缘硬质细管AB竖直固定在匀强电场中．环的半径R=0.30m，离水平面地面的距离为h=5.0m，一带正电的小球从管的上端口A由静止释放，小球大小略小于管的直径，它与管间摩擦不计，小球在电场中受到的电场力大小为重力的一半．求：
（1）小球运动到管口B时的速度大小；
（2）小球着地点与管的下端口B的水平距离；
（3）若使带电小球离开环B点瞬间，突然撤去匀强电场，为了能使带电小球向右做匀速直线运动，可以加垂直纸面方向的匀强磁场，试求磁场的方向以及磁感应强度B和原匀强电场强度E的比． （g=lOm/s²）

Answer 1

分析：（1）小球从A运动到管口B的过程中，重力做功mgR，电场力做功FR=

1

2

mgR，根据动能定理求解小球运动到管口B时的速度大小；
（2）小球离开管口B后，受到重力和电场力作用，由于这两个力都是恒力，可运用运动的分解法研究：水平方向在电场力作用下做匀加速运动，竖直方向做自由落体运动，由高度h=

1

2

gt2，求出时间，水平距离x=v_Bt+

1

2

at2，a=

F

m

=

g

2

．
（3）撤去匀强电场，为了能使带电小球向右做匀速直线运动，洛伦兹力必须与重力平衡，由左手定则判断磁场的方向，由平衡条件求解B和E的比值．

解答：解：（1）小球从A运动到管口B的过程中，只有重力和电场力做功，根据动能定理得
   mg+FR=

1

2

m

v

2 B

而由题意，电场力F=

1

2

mg
则联立解得，vB=

3gR

=3m/s
（2）小球离开管口B后，受到重力和电场力作用，竖直方向做自由落体运动，
由h=

1

2

gt2得  t=

2h g

水平方向做匀加速运动，设加速度大小为a，位移为x．
则a=

F

m

=

1

2

g
  x=v_Bt+

1

2

at2=

6Rh

+

h

2

代入数据解得，x=5.5m
（3）为了能使带电小球向右做匀速直线运动，洛伦兹力必须与重力平衡，根据左手定则判断可知，磁场方向向里，且有
  mg=qv_BB
又qE=

1

2

mg
解得

E

B

=

2

3

答：
（1）小球运动到管口B时的速度大小是3m/s；
（2）小球着地点与管的下端口B的水平距离是5.5m；
（3）磁场的方向向里，磁感应强度B和原匀强电场强度E的比值为2：3．

点评：小球在管中运动过程，重力和电场力做功，由动能定理研究通过B点的速度．小球在电场和重力场的复合场中时，运用运动的分解法求解水平位移．