题目内容
2.一物理兴趣小组在实验室用如图1所示的装置“研究平抛运动的规律”,实验步骤如下:①用图钉把白纸订在竖直木板上;
②把斜槽固定在紧靠木板的左上角,且使其末端切线水平;
③记下小铁球飞出时初始位置D,并凭眼观测过O画水平线作为x轴;
④把水平木条靠在竖直木板上,让小铁球从斜槽适当的位置由静止滚下,观察小铁球在木条上的落点,并在白纸上标出相应的点,得到小铁球运动过程中的一个位置;
⑤把水平木条向下移动,重复④的操作,让小铁球从斜槽上相同位置由静止滚下,得到小铁球运动过程中的多个位置;
⑥从木板上取下白纸,…
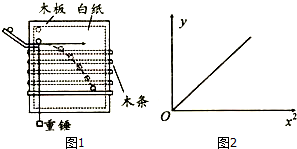
(1)上述①到⑥的步骤中,有错误的是步骤③,应改为过O点作重锤线的垂线为x轴;
(2)根据画出的轨迹测出小铁球多个位置的坐标(x,y),画出y-x2图象如图2所示,图线是一条过原点的
直线,说明小铁球运动的轨迹形状是抛物线;若已知该直线的斜率为k,重力加速度为g,则小铁球从轨道末端飞出的速度v0=$\sqrt{\frac{g}{2k}}$.
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合平抛运动的轨道求出y与x2的关系,通过图线的斜率和重力加速度求出初速度.
解答 解:(1)上述①到⑥的步骤中,有错误的是步骤③,应改为过O点作重锤线的垂线为x轴.
(2)水平方向上,有:x=v0t,竖直方向上,有:y=$\frac{1}{2}$gt2,
可得y=$\frac{g}{2{v}_{0}^{2}}$x2,可知小铁球的运动轨迹为抛物线.
根据y与x2表达式知,图线的斜率k=$\frac{g}{2{v}_{0}^{2}}$,
解得:v0=$\sqrt{\frac{g}{2k}}$.
故答案为:(1)③,过O点作重锤线的垂线为x轴;(2)抛物线,$\sqrt{\frac{g}{2k}}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式进行求解.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 质点是不存在的,引入这概念没有意义 | |
| B. | 物体在运动过程中,路程总等于位移的大小 | |
| C. | 加速度减小,速度一定也减小 | |
| D. | 速度变化越快,加速度越大 |
17. 如图所示,在三维直角坐标系中,有一电流沿y轴正方向流动,该电流在x轴上的P点产生的磁场方向是( )
如图所示,在三维直角坐标系中,有一电流沿y轴正方向流动,该电流在x轴上的P点产生的磁场方向是( )
 如图所示,在三维直角坐标系中,有一电流沿y轴正方向流动,该电流在x轴上的P点产生的磁场方向是( )
如图所示,在三维直角坐标系中,有一电流沿y轴正方向流动,该电流在x轴上的P点产生的磁场方向是( )| A. | +x方向 | B. | -x方向 | C. | +z方向 | D. | -z方向 |
7. 如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )
如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )
 如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )
如图所示,在粗糙绝缘的水平面上固定一带负电的点电荷P,在M点无初速释放一带有恒定电荷的小物块,小物块在P的电场中运动到N点静止,则从M点运动到N点的过程中,下面说法正确的是( )| A. | 小物块所带电荷为正电荷 | |
| B. | 小物块共有的电势能逐渐增大 | |
| C. | 小物块的加速度先减小后增大 | |
| D. | 小物块电势能的减少量等于克服摩擦力做的功 |
14.某灯泡的冷态电阻为10欧,该灯泡工作在额定电压6V时,发现灯泡的电流比0.6A要小,其主要原因是( )
| A. | 灯丝变长 | B. | 灯丝变粗 | C. | 灯丝变细 | D. | 电阻率变大 |
11. 电动公交车主要是指纯电动公交车,全部使用电能行驶,该类公交车噪音小,行驶稳定性高,并且实现零排放.如图所示,某电动公交车做匀加速直线运动,在10s内,速度由0增加到20m/s,则该电动公交车的加速度为( )
电动公交车主要是指纯电动公交车,全部使用电能行驶,该类公交车噪音小,行驶稳定性高,并且实现零排放.如图所示,某电动公交车做匀加速直线运动,在10s内,速度由0增加到20m/s,则该电动公交车的加速度为( )
 电动公交车主要是指纯电动公交车,全部使用电能行驶,该类公交车噪音小,行驶稳定性高,并且实现零排放.如图所示,某电动公交车做匀加速直线运动,在10s内,速度由0增加到20m/s,则该电动公交车的加速度为( )
电动公交车主要是指纯电动公交车,全部使用电能行驶,该类公交车噪音小,行驶稳定性高,并且实现零排放.如图所示,某电动公交车做匀加速直线运动,在10s内,速度由0增加到20m/s,则该电动公交车的加速度为( )| A. | 0.5m/s2 | B. | 1m/s2 | C. | 2m/s2 | D. | 4m/s2 |
 如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.用手水平托住D球并保持D球静止状态,此时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)求:
如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.用手水平托住D球并保持D球静止状态,此时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)求: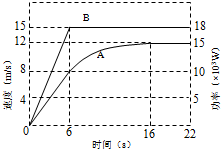 一辆机动车在平直的公路上由静止启动开始做直线运动,图中图线A表示该车运动的速度和时间的关系,图线B表示车的功率和时间的关系.设车在运动过程中阻力不变,车在6s末前做匀加速运动,在16s末开始匀速运动.可知车的质量为562.5kg,车从静止开始到16s末内的总位移为129m.
一辆机动车在平直的公路上由静止启动开始做直线运动,图中图线A表示该车运动的速度和时间的关系,图线B表示车的功率和时间的关系.设车在运动过程中阻力不变,车在6s末前做匀加速运动,在16s末开始匀速运动.可知车的质量为562.5kg,车从静止开始到16s末内的总位移为129m.