题目内容
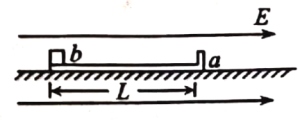
【题目】如图,光滑水平面上静置质量为m，长为L的绝缘板a,绝缘板右端园定有竖直挡板,整个装置置于水平向右的匀强电场中.现将一质量也为m、带电量为q(q>0)的物块b置于绝缘板左端(b可视为质点且初速度为零)，已知匀强电场的场强大小为E=3μmg/q，物块与绝缘板板间动摩擦数为μ(设最大静摩擦力等于滑动摩擦力)，物块与绝缘板右端竖直挡板碰撞后a、b速度交换,且碰撞时间极短可忽略不计,物块带电量始终保持不变,重力加速度为g。求：
(1)物块第一次与挡板碰撞前瞬间物块的速度大小;
(2)物块从置于绝缘板到第二次与挡板碰撞过程中,电场力所做的功W。
【答案】(1) 
(2) 
【解析】
(1)根据同向运动的物体位移之差等于相对位移，牛顿第二定律结合运动学公式求解.
(2)碰撞过程满足动量守恒，往返运动再次碰撞的过程依然用牛顿第二定律结合运动学公式求解位移；恒力做功由功的定义式处理.
(1)由题知：物块b受恒定电场力
对两物体由牛顿第二定律，物块b：
，得
对绝缘板a：
，得
设历时t1物块第一次与挡板碰撞，有：
，得：
则物块第一次与挡板碰撞前瞬时，物块的速度大小
解得：
(2)绝缘板a的速度大小
，解得：
物块对地的位移大小为
，有
物块与绝缘板的右端竖直挡板发生弹性碰撞后，二者速度交换
则物块的速度为
，绝缘板的速度大小为
对物块b：
，有
设历时t2，二者达到共同速度v，有：
，
解得：
二者相对位移大小为x，有
，解得：
物块对地的位移大小为x2，有
，解得：
设历时t3物块第二次与挡板碰撞，有：
，得：
物块对地的位移大小为x3，有
，解得：
故物块的总位移
得：
根据功的定义
解得：
练习册系列答案
阅读快车系列答案
相关题目
