题目内容
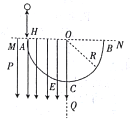
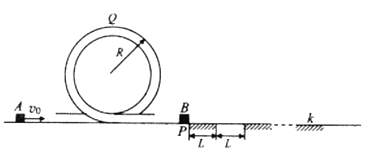
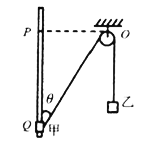
【题目】如图所示，不可伸长的轻绳通过定滑轮将物块甲、乙（均可视为质点）连接，物块甲套在固定的竖直光滑杆上，用外力使两物块静止，轻绳与竖直方向夹角
，然后撤去外力，甲、乙两物块从静开始运动，物块甲恰能上升到最高点P，P点与滑轮上缘O在同一水平线上，甲、乙两物块质量分别为m、M，
，重力加速度为g，不计空气阻力，不计滑轮的大小和摩擦。设物块甲上升到最高点P时加速度为a，则下列说法正确的是（ ）
A. M=2m
B. M=3m
C. a=g
D. a=0
【答案】AC
【解析】设QP间的距离为h，OQ间的绳长
；则乙下降的高度为
则根据机械能守恒定律可知，mgh=Mgh′；解得：M=2m；故A正确，B错误。甲上升到最高点P时。由于不受摩擦力，所以在竖直方向上只受重力，水平方向上弹力与绳子的拉力平衡，因此甲的加速度为g，故C正确，D错误。故选AC。
练习册系列答案
相关题目
