题目内容
14.写出两个质子(${\;}_{1}^{1}$H)与两个中子(${\;}_{0}^{1}$n)聚变生成一个氦核(${\;}_{2}^{4}$He)的核反应方程式2${\;}_{1}^{1}$H+2${\;}_{0}^{1}$n→${\;}_{2}^{4}$He.若质子的质量为m1、中子的质量为m2、氦核的质量为m3,则反应中放出的能量为$(2{m}_{1}+2{m}_{2}-{m}_{3}){c}^{2}$.分析 结合质量数守恒与核电荷数守恒即可求出核反应方程;先求出核反应中质量亏损,再由爱因斯坦质能方程,反应释放的核能△E=△m•c2,从而即可求解.
解答 解:两个质子(${\;}_{1}^{1}$H)与两个中子(${\;}_{0}^{1}$n)聚变生成一个氦核(${\;}_{2}^{4}$He),其核反应方程为:2${\;}_{1}^{1}$H+2${\;}_{0}^{1}$n→${\;}_{2}^{4}$He.
质子的质量为m1、中子的质量为m2、氦核的质量为m3,则反应中放出的能量:
E=△m•c2=$(2{m}_{1}+2{m}_{2}-{m}_{3}){c}^{2}$
故答案为:2${\;}_{1}^{1}$H+2${\;}_{0}^{1}$n→${\;}_{2}^{4}$He,$(2{m}_{1}+2{m}_{2}-{m}_{3}){c}^{2}$
点评 本题考查应用质能方程研究核反应中质量亏损的能力.另外要知道核反应向平均结合能增大的方向进行,要释放能量.

练习册系列答案
相关题目
2.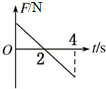 静止在光滑水平面上的物体在水平力F作用下开始运动,力F随时间的变化如图所示,关于物体的运动情况,正确的描述是( )
静止在光滑水平面上的物体在水平力F作用下开始运动,力F随时间的变化如图所示,关于物体的运动情况,正确的描述是( )
 静止在光滑水平面上的物体在水平力F作用下开始运动,力F随时间的变化如图所示,关于物体的运动情况,正确的描述是( )
静止在光滑水平面上的物体在水平力F作用下开始运动,力F随时间的变化如图所示,关于物体的运动情况,正确的描述是( )| A. | t=2 s时刻物体速度为0 | |
| B. | 4 s末物体回到出发点 | |
| C. | 在0~4 s时间内水平力F的总冲量为0 | |
| D. | 在0~2 s时间内物体做匀减速运动,在2 s~4 s时间内物体做匀加速运动 |
19.一质点从t=0开始沿x轴做直线运动,其位置坐标与时间的关系为x=2t3-8t+1(x和t的单位分别为m和s),则下列说法中正确的是( )
| A. | 质点一直向x轴正方向运动 | |
| B. | 质点做匀变速直线运动 | |
| C. | 质点在第2s内的平均速度大小为6m/s | |
| D. | 质点在前2s内的位移为零 |
6.关于欧姆定律的相关内容,下列说法中正确的是( )
| A. | 从R=$\frac{U}{I}$可知:对于一个确定的导体来说,如果通过的电流越大,则导体两端的电压也越大 | |
| B. | 从I=$\frac{U}{R}$知:导体中的电流强度跟导体两端的电压成正比,跟导体的电阻成反比 | |
| C. | 从R=$\frac{U}{I}$可知:导体的电阻跟导体两端的电压成正比,跟导体中的电流强度成反比 | |
| D. | 对一段确定的导体来讲,比值$\frac{U}{I}$恒定,不随U或I的改变而改变 |
14.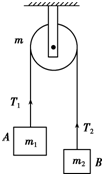 如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )
如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )
 如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )
如图所示,一不可伸长的轻质细绳跨过定滑轮后,两端分别悬挂质量为m1和m2的物体A和B.若滑轮有一定大小,质量为m且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的磨擦.设细绳对A和B的拉力大小分别为T1和T2,已知下列四个,关于T1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析,判断正确的表达式是( )| A. | T1=$\frac{(m+2{m}_{2}){m}_{1}g}{m+2({m}_{1}+{m}_{2})}$ | B. | T1=$\frac{(m+2{m}_{1}){m}_{1}g}{m+4({m}_{1}+{m}_{2})}$ | ||
| C. | T1=$\frac{(m+4{m}_{2}){m}_{1}g}{m+2({m}_{1}+{m}_{2})}$ | D. | T1=$\frac{(m+4{m}_{1}){m}_{2}g}{m+4({m}_{1}+{m}_{2})}$ |
 用两根绳子吊起一个重物,物体的重力为G=100N,如图所示(sin37°=0.6,sin53°=0.8)求:
用两根绳子吊起一个重物,物体的重力为G=100N,如图所示(sin37°=0.6,sin53°=0.8)求: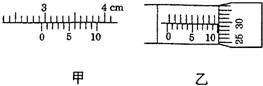 读出如图所示的游标卡尺(游标尺上有10个等分刻度)和螺旋测微器的示数,图甲的读数为2.96cm,图乙的读数为10.295mm.
读出如图所示的游标卡尺(游标尺上有10个等分刻度)和螺旋测微器的示数,图甲的读数为2.96cm,图乙的读数为10.295mm. 质量为3kg、长为0.5m的木板B静止于光滑水平面上,物块A质量也为3kg,停在B的左端.质量为1kg的小球用长为0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2m,最后物块未脱离木板.物块与小球可视为质点,不计空气阻力,取重力加速度为g=10m/s2,试求:
质量为3kg、长为0.5m的木板B静止于光滑水平面上,物块A质量也为3kg,停在B的左端.质量为1kg的小球用长为0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2m,最后物块未脱离木板.物块与小球可视为质点,不计空气阻力,取重力加速度为g=10m/s2,试求: