题目内容
14.一列简谐横波沿一根弹性绳传播,某一时刻质点a处于波峰,另一质点b正处于平衡位置,a,b的平衡位置相距14m,从此时刻开始,质点b经0.14s刚好第二次到达波峰,求这列波最大的传播速度可能是多少?分析 由题意可明确该波的周期,再由周期明确最大波长,由v=$\frac{λ}{T}$可求得最大传播速度.
解答 解:由题意可知,波的周期为T=2×0.14s=0.28s;
ab间相隔可能是n+$\frac{1}{4}$λ或为:n+$\frac{3}{4}$λ;因距离一定,则当距离为$\frac{λ}{4}$时波速最大;此时波长λ=4×14m=56m;
最大波速v=$\frac{λ}{T}$=$\frac{56}{0.28}$m/s=200m/s;
答:最大波速为200m/s.
点评 本题考查波多解性,要注意明确波在传播空间上和时间上均具有周期性,在解题中要注意认真体会.

练习册系列答案
相关题目
2. 如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )
如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )
 如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )
如图所示为二极管所构成的逻辑电路,A、B为输入端,Y为输出端(设输入、输出端高电位为1,低电位为0),则下列说法正确的是( )| A. | A=0,B=0时,Y=1 | B. | A=0,B=1时,Y=0 | C. | A=1、B=0时,Y=1 | D. | A=1、B=1时,Y=1 |
1. 如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,CO为一根轻杆,转轴C在AB中点D的正下方,AOB在同一水平面内.∠AOB=120°,∠COD=60°.若在O点处悬挂一个质量为m的物体,则平衡后绳AO所受的拉力和杆OC所受的压力分别为( )
如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,CO为一根轻杆,转轴C在AB中点D的正下方,AOB在同一水平面内.∠AOB=120°,∠COD=60°.若在O点处悬挂一个质量为m的物体,则平衡后绳AO所受的拉力和杆OC所受的压力分别为( )
 如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,CO为一根轻杆,转轴C在AB中点D的正下方,AOB在同一水平面内.∠AOB=120°,∠COD=60°.若在O点处悬挂一个质量为m的物体,则平衡后绳AO所受的拉力和杆OC所受的压力分别为( )
如图所示,A、B为竖直墙面上等高的两点,AO、BO为长度相等的两根轻绳,CO为一根轻杆,转轴C在AB中点D的正下方,AOB在同一水平面内.∠AOB=120°,∠COD=60°.若在O点处悬挂一个质量为m的物体,则平衡后绳AO所受的拉力和杆OC所受的压力分别为( )| A. | mg,$\frac{1}{2}$mg | B. | $\frac{\sqrt{3}}{3}$mg,$\frac{2\sqrt{3}}{3}$mg | C. | $\frac{1}{2}$mg,mg | D. | $\frac{2\sqrt{3}}{3}$mg,$\frac{2\sqrt{3}}{3}$mg |
8.如图,在同一竖直平面内,距地面不同高度的地方,以不同的水平速度同时抛出两个小球,则( )

| A. | 两球一定不能在空中相遇 | |
| B. | 两球落地时间可能相等 | |
| C. | 两球抛出到落地的水平距离有可能相等 | |
| D. | 两球运动的水平距离与抛出点的高度无关 |
5. 如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )
如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )
 如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )
如图所示,物体沿水平面内的四分之一圆弧轨道由A点运动到B点的过程中速度大小保持不变,则该物体( )| A. | 做匀速运动 | B. | 做匀变速曲线运动 | ||
| C. | 受到的合外力为零 | D. | 加速度大小保持不变 |
6.将一只小球竖直上抛,当它到达最高点时速度为零,加速度的方向是( )
| A. | 方向从向上变为向下 | B. | 方向从向下变向上 | ||
| C. | 方向向上 | D. | 方向向下 |
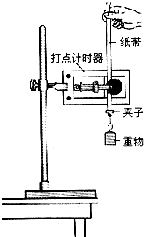 某同学在做“验证机械能守恒定律”的实验中,列出下面一些步骤:
某同学在做“验证机械能守恒定律”的实验中,列出下面一些步骤: