题目内容
3. 两颗地球工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中正确的是( )
两颗地球工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下判断中正确的是( )| A. | 这2颗卫星的加速度大小相等,均为$\frac{{R}^{2}g}{{r}^{2}}$ | |
| B. | 卫星1由位置A第一次运动到位置B所需的时间为$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$ | |
| C. | 卫星1向后喷气,瞬间加速后,就能追上卫星2 | |
| D. | 卫星1向后喷气,瞬间加速后,绕地运行周期变长 |
分析 由G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=mω2r=m($\frac{2π}{T}$)2r=ma,可得出r相同则速度v大小相等,v变大则r变大(做离心运动),再结合$\frac{GMm}{{R}^{2}}$=mg,即GM=gR2(黄金代换),即可求解
解答 解:A、根据F合=ma得,
对卫星有$\frac{GMm}{{r}^{2}}$=ma,
取地面一物体由$\frac{GMm}{{R}^{2}}$=mg,
联立解得a=$\frac{{R}^{2}}{{r}^{2}}$g,故A正确.
B、根据G$\frac{Mm}{{r}^{2}}$=m($\frac{2π}{T}$)2r①,
又GM=gR2②,
t=$\frac{1}{6}$T③,
联立①②③可解得t=$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$.故B正确;
C、D、若卫星1向后喷气,则其速度会增大,卫星1将做离心运动,轨道半径增大,所以周期增大,卫星1不可能追上卫星2.故C错误,D正确;
故选:ABD
点评 关于做圆周运动的卫星类问题,要灵活运用两个公式G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=mω2r=m($\frac{2π}{T}$)2r=ma、$\frac{GMm}{{R}^{2}}$=mg,注意卫星若加速则做离心运动,减速则做向心运动.

练习册系列答案
相关题目
14. 如图所示,固定在水平地面上的斜面体顶端安装一定滑轮,两物块P、Q用轻绳连接并跨过定滑轮,P悬于空中,Q放在斜面上,均处于静止状态.不计滑轮的质量和绳子与滑轮间的摩擦,当用水平向右的恒力推Q时,P、Q仍静止不动,则( )
如图所示,固定在水平地面上的斜面体顶端安装一定滑轮,两物块P、Q用轻绳连接并跨过定滑轮,P悬于空中,Q放在斜面上,均处于静止状态.不计滑轮的质量和绳子与滑轮间的摩擦,当用水平向右的恒力推Q时,P、Q仍静止不动,则( )
 如图所示,固定在水平地面上的斜面体顶端安装一定滑轮,两物块P、Q用轻绳连接并跨过定滑轮,P悬于空中,Q放在斜面上,均处于静止状态.不计滑轮的质量和绳子与滑轮间的摩擦,当用水平向右的恒力推Q时,P、Q仍静止不动,则( )
如图所示,固定在水平地面上的斜面体顶端安装一定滑轮,两物块P、Q用轻绳连接并跨过定滑轮,P悬于空中,Q放在斜面上,均处于静止状态.不计滑轮的质量和绳子与滑轮间的摩擦,当用水平向右的恒力推Q时,P、Q仍静止不动,则( )| A. | Q受到的摩擦力一定变大 | B. | Q受到的摩擦力一定变小 | ||
| C. | 轻绳上的拉力一定变小 | D. | Q对斜面的压力一定变大 |
11.作用于同一点的两个力大小分别为F1=10N,F2=6N,这两个力的合力F与F1的夹角为θ,则θ可能为( )
| A. | 0° | B. | 30° | C. | 60° | D. | 120° |
18.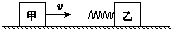 如图所示,甲木块的质量为m,以速度v沿光滑水平地面向前运动,正前方有一静止的、质量为2m的乙木块,乙上连有一轻质弹簧.甲木块与弹簧接触后( )
如图所示,甲木块的质量为m,以速度v沿光滑水平地面向前运动,正前方有一静止的、质量为2m的乙木块,乙上连有一轻质弹簧.甲木块与弹簧接触后( )
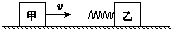 如图所示,甲木块的质量为m,以速度v沿光滑水平地面向前运动,正前方有一静止的、质量为2m的乙木块,乙上连有一轻质弹簧.甲木块与弹簧接触后( )
如图所示,甲木块的质量为m,以速度v沿光滑水平地面向前运动,正前方有一静止的、质量为2m的乙木块,乙上连有一轻质弹簧.甲木块与弹簧接触后( )| A. | 当弹簧被压缩到最短时弹性势能为$\frac{1}{3}m{v^2}$ | |
| B. | 甲、乙两木块的动量分别守恒 | |
| C. | 甲、乙两木块和弹簧所组成的系统能量守恒 | |
| D. | 甲、乙两木块所组成的系统动量守恒 |
12.人造卫星在离地心为r的圆轨道上做匀速圆周运动,地球质量为M,地球半径为R,人造卫星质量为m,人造卫星绕地球的角速度为ω,万有引力恒量为G,地球表面重力加速度为g,计算人造卫星所受的向心力的式子正确的是( )
| A. | mg | B. | $\frac{GMm}{{{{(R+r)}^2}}}$ | C. | mω2R | D. | $\frac{{mg{R^2}}}{r^2}$ |
13.关于电流的下列说法中,正确的是( )
| A. | 电路中的电流越大,表示通过导体横截面的电量越多 | |
| B. | 在相同时间内,通过导体截面的电量越多,导体中的电流就越大 | |
| C. | 通电时间越长,电流越大 | |
| D. | 因为电流有方向,所以电流是矢量 |

 重20N的物块,放在水平桌面上,用F=8N的水平拉力可以使其做匀速直线运动,求:
重20N的物块,放在水平桌面上,用F=8N的水平拉力可以使其做匀速直线运动,求: