题目内容
4.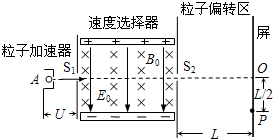 如图所示,左侧为粒子加速器,A中产生粒子的速度从0到某一很小值之间变化,粒子的质量为m,电荷量为q(q>0),经过电压U加速,穿过狭缝S1进入中间的速度选择器.选择器中的电场强度为E0,磁感应强度为B0.粒子穿过狭缝S2进入右侧的粒子偏转区,最后要求落到屏上的P点.已知偏转区宽度为L,P点离O点的距离为L/2,不计重力.
如图所示,左侧为粒子加速器,A中产生粒子的速度从0到某一很小值之间变化,粒子的质量为m,电荷量为q(q>0),经过电压U加速,穿过狭缝S1进入中间的速度选择器.选择器中的电场强度为E0,磁感应强度为B0.粒子穿过狭缝S2进入右侧的粒子偏转区,最后要求落到屏上的P点.已知偏转区宽度为L,P点离O点的距离为L/2,不计重力.(1)求粒子刚进入狭缝S1时速度v1的大小(不计粒子在A中的速度);
(2)求粒子通过速度选择器刚进入狭缝S2时速度v2的大小;
(3)请你提出一种简单方案,使粒子在偏转区内从S2飞入恰好能打到屏上的P点.
要求:①在答卷图上的粒子偏转区内画出示意图(注意规范);②求出你所用方案中涉及到的一个最关键的物理量的大小.
分析 (1)粒子在电场中加速,应用动能定理可以求出粒子的速度.
(2)粒子在速度选择器中做匀速直线运动,应用平衡条件可以求出粒子速度.
(3)可以在偏转区加电场或磁场,使粒子在偏转区偏转,然后打在P点,应用类平抛运动规律或牛顿第二定律分析答题.
解答 解:(1)粒子在加速器内加速,由动能定理得:qU=$\frac{1}{2}$mv12-0,
解得,粒子刚进入狭缝S1时速度v1的大小:v1=$\sqrt{\frac{2qU}{m}}$;
(2)粒子在速度选择器内做直线运动满足:qE0=qv2B0,
可得刚进入狭缝S2时速度v2的大小:v2=$\frac{{E}_{0}}{{B}_{0}}$;
(3)方案一:在粒子偏转区加匀强电场,示意图:
粒子在匀强电场中做类平抛运动:
L=v2t $\frac{1}{2}$L=$\frac{1}{2}$$\frac{qE}{m}$t2 解得:E=$\frac{m{E}_{0}^{2}}{qL{B}_{0}^{2}}$;
方案二:在粒子偏转区加匀强磁场,示意图:
粒子在匀强磁场中做匀速圆周运动,由几何知识得:
r2=L2+(r-$\frac{L}{2}$)2,解得:r=$\frac{5}{4}$L,
粒子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qv2B=m$\frac{{v}_{2}^{2}}{r}$,解得:B=$\frac{4m{E}_{0}}{5qL{B}_{0}}$;
答:(1)粒子刚进入狭缝S1时速度v1的大小为$\sqrt{\frac{2qU}{m}}$;
(2)粒子通过速度选择器刚进入狭缝S2时速度v2的大小为$\frac{{E}_{0}}{{B}_{0}}$;
(3)使粒子在偏转区内从S2飞入恰好能打到屏上的P点.
①如图所示;②加电场时,电场强度:$\frac{m{E}_{0}^{2}}{qL{B}_{0}^{2}}$;加磁场时,磁感应强度:$\frac{4m{E}_{0}}{5qL{B}_{0}}$.
点评 本题考查了粒子在磁场、复合场中的运动,分析清楚粒子运动过程是解题的关键,应用动能定理、平衡条件、类平抛运动与牛顿第二定律可以解题.

| A. | 元电荷就是电子 | |
| B. | 元电荷是表示跟电子所带电量数值相等的电量 | |
| C. | 体积很小的带电体就是点电荷 | |
| D. | 如果地球带了电,地球不能看成点电荷 |
(1)试按如图1原理图在如图2实物图中画线连接成实验电路.

(2)一位同学记录的6组数据如下,试根据这些数据在如图3中画出U-I图线.
| I×10-3(A) | 2.0 | 3.5 | 4.2 | 6.0 | 7.1 | 7.9 |
| U(V) | 1.42 | 1.35 | 1.33 | 1.25 | 1.20 | 1.16 |
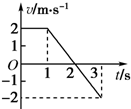
| A. | 在1~3s内质点做减速直线运动 | |
| B. | 在1~3s内质点的加速度a=-2m/s2 | |
| C. | 在2~3s内质点的运动方向与规定的正方向相反,加速度方向同1~2s内的加速度方向相同 | |
| D. | 在0~3s内质点做单一方向的直线运动 |
| A. | 2s内 | |
| B. | 刘翔以12.91s获得雅典奥运会110m栏冠军 | |
| C. | 第2s内 | |
| D. | 物体在第5s末到达终点 |
 如图所示,在“研究力的合成”实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套.实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条.某同学认为在此过程中必须注意以下几项:
如图所示,在“研究力的合成”实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套.实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条.某同学认为在此过程中必须注意以下几项: